Eccoci all’articolo più importante della serie.
Abbiamo parlato degli acciai e abbiamo visto le tipologie di armature simulate nei test: ora non resta che combinare le informazioni, leggere i resoconti dei test e…
…trarne le conclusioni.
I test riportati e i dati utilizzati provengono perlopiù dal libro The Knight and the Blast Furnace del dottor Alan Williams (che ringrazio per l’assistenza fornita via e-mail), ma sono stati integrati e controllati sfruttando ulteriori informazioni provenienti da The Great Warbow di Robert Hardy e Matthew Strickland e da Weapons & Warfare in Renaissance Europe di Bert Hall. Più altre fonti minori, lette solo a scopo confermativo, che non vale la pena citare.
Le armi da simulare e il macchinario utilizzato
Le principali minacce per le armature sono le frecce e i proiettili. Le frecce sono pericolose perché hanno sia molta energia cinetica che una superficie di impatto molto piccola, il che si traduce in un’alta pressione che può perforare la corazza. Una lama di spada o di alabarda a pari energia cinetica avrà una superficie di impatto molto superiore il che si traduce in una pressione nettamente minore.
Superficie di impatto e pressione esercitata sono inversamente proporzionali: al raddoppiare della superficie si dimezza la pressione esercitata dalla forza applicata secondo la normale (ovvero perpendicolarmente).
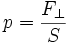 |
Tutti test considerati utilizzano l’energia cinetica (in Joule) per quantificare la violenza del colpo. L’energia cinetica, come ricorderete, è determinata dalla massa del corpo e dalla velocità. In parole povere: un macigno che vi piomba addosso a 100 km/h vi farà più male di un sassolino che vi percuote a 20 km/h.
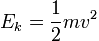 |
Come potete vedere dalla formula l’energia raddoppia al raddoppiare della massa e quadruplica al raddoppiare della velocità. Potete anche facilmente intuire che se serve una pressione X a penetrare una data corazza, allora la forza disponibile deve crescere con la superficie su cui si applica (non necessariamente con l’esatta proporzione, nel caso dei proiettili e della formula di Krupp, ma ne parleremo un’altra volta).
Per questo motivo la seconda minaccia principale presa in considerazione sono i proiettili: seppure l’energia cinetica necessaria per perforare sia molto superiore rispetto a quella delle frecce, i proiettili hanno il vantaggio di poter disporre di enormi quantità di energia cinetica per compensare lo svantaggio.
Anche le lame sono state testate, ma in modo meno approfondito, principalmente perché perfino con una lama di soli 4 cm di lunghezza si è visto che penetrare corazze era fuori dalla portata di chiunque …a meno che non fosse un bestione con tricipiti grossi come meloni e possibilmente armato di alabarda, il che in un fantasy non è da escludere.
 |
| Rosand IFW5, ma per gli amici è Rosand IFW5 |
I test sono stati condotti con il Rosand IFW5, la macchina infernale, che permette di scegliere “l’arma” e il carico da applicare in caduta. Poi il tutto precipita e sfonda (o almeno prova a sfondare) quello che gli hai messo sotto. Usando un carico posizionato dietro la lama/punta/proiettile in caduta, si aumenta in modo proporzionale sia la quantità di moto che l’energia cinetica, grossomodo (per un proiettile, come da formula di Krupp, la distinzione è irrilevante). Con questo attrezzo un ingegnere meccanico può passare un bel fine settimana sfondando fogli di acciaio, giubbotti di cuoio, scatole di preservativi e dispense del corso di macchine a fluido.
 |
| Alcuni oggetti usati per le simulazioni nei Test |
Tre delle armi usate nelle simulazioni, tutte di ottimo acciaio: una lama (lunga 4 cm), una freccia (con un design da sfondamento, come le più pesanti frecce da guerra o i dardi da balestra, punta da 40 gradi) e un proiettile (largo 20 mm). Sul proiettile simulato torneremo più avanti nel corso dell’articolo, con alcune considerazioni utili per chi sta storcendo il naso pensando “come sarebbe a dire acciaio e non piombo morbido?“.
La simulazione delle armature
Nel caso delle corazze non è stato possibile utilizzare reali armature per i test, dato che questo avrebbe comportato il grave danneggiamento di decine di reperti di notevole valore storico, dovendo agire su un gran quantità di combinazioni di spessori, scorie, percentuali di carbonio, tipologie di acciaio e durezze.
Partendo dai dati raccolti sulla durezza e la composizione microscopica delle armature reali è però possibile costruire un modello che dia una stima attendibile del comportamento di queste armature a partire da test compiuti su fogli di acciaio di qualità note, ma privi di valore storico.
Le tabelle dei test con le frecce e i proiettili contengono dati estrapolati a partire dai dati sperimentali ottenuti con dell’acciaio dolce (mild steel) spesso 2 mm, col 0,15% di carbonio, privo di scorie, di durezza 152 VPH e tenacità alla frattura 235 KJ/m2. La durezza può non sembrare molto alta, ma come ricorderete quello che conta davvero è la tenacità alla frattura perché senza frattura non può nemmeno avvenire la penetrazione.
Quell’acciaio è stato considerato come termine di paragone per tutti gli altri. Conoscendo le relazioni che intercorrono tra la percentuale di carbonio, il contenuto in scorie e la tenacità alla frattura, Alan Williams ha suddiviso gli acciai in fasce di qualità attribuendo a ogni fascia un coefficiente W da moltiplicare con i risultati ottenuti sull’acciaio morbido (W = 1,0) per stimare la loro resistenza ai colpi.
Fasce di qualità
I – Ferro da munizione (scorie 3-4%, senza carbonio)
120-150 KJ/m2, W = 0,5
esempio: il ferraccio delle armature da picchiere prodotte in massa nel Seicento.
II – Acciaio con poco carbonio (scorie 1%, carbonio 0,3%)
180-210 KJ/m2, W = 0,75
esempio: le armature da fanteria di Norimberga.
III – Acciaio con un livello medio di carbonio (scorie < 1%, carbonio 0,6%)
240-260 KJ/m2, W = 1,1
esempio: le armature milanesi del XV-XVI secolo o quelle di Greenwich di inizio XVI secolo
IV – Acciaio con un livello medio di carbonio, indurito (scorie 0,5% circa, carbonio 0,6%)
300-500+ KJ/m2, W = 1,5 e oltre
esempio: armature provenienti da Innsbruck, Augsburg, Landshut e Greenwich (dopo il 1560), con carburi formati da martensite invece che da perlite.
I test con le frecce
I test con le frecce erano volti a simulare frecce da guerra, con punte da sfondamento forgiate in un acciaio molto duro per non deformarsi all’impatto: la punta vista in foto sembra soddisfare pienamente i requisiti. L’energia disponibile con le frecce tirate dai veri archi può variare dai 46 ai 140 J circa.
Gli unici archi interessanti sono però quelli da guerra da 100-150 libbre, non i deboli archi da 50-70 libbre usati nei circoli di tiro. Un arco lungo da 150 libbre può lanciare una freccia da 3,3 once (96 grammi) a 250 metri con una energia iniziale di 134 J e una energia all’impatto di 90 J. O frecce più leggere, da poco meno di 2 once, capaci però di volare fino a 330 metri con un’energia iniziale di 111 J e una finale di 64 J.
Una balestra può inviare dardi più pesanti delle comuni frecce a velocità simili, fornendo tra i 100 e i 200 J, forse addirittura 250 J con dardi da 5 once (140 grammi).
La freccia simulata ha iniziato a penetrare un foglio di acciaio morbido da 1 mm con 30 J e uno da 1,5 mm con 80 J. Ma se si vogliono ottenere anche 40 mm di penetrazione, ovvero una “ferita decente” tale da poter dire che l’armatura è stata sconfitta, l’energia aumenta rispettivamente a 55 J e a 110 J. In particolare l’energia necessaria all’aumentare dello spessore non aumenta proporzionalmente allo spessore, ma con una potenza di 1,6.
In parole povere: al raddoppiare dello spessore triplica l’energia necessaria.
| Spessore | Moltiplicatore |
| 1 | 1 |
| 1,5 | 1,9 |
| 2 | 2,9 |
| 2,5 | 4,9 |
| 3 | 5,5 |
| 3,5 | 7 |
| 4 | 8,6 |
Tabella di Resistenza alle Frecce
1 mm 2 mm 3 mm 4 mm Normale 55 J 175 J 300 J 475 J Impatto 30° 66 J 210 J 360 J 570 J Impatto 45° 78 J 250 J 425 J 670 J
Le frecce usate nei test contro le piastre riportati qui sopra credo siano quelle con la punta da 40 gradi, da sfondamento (quella da 18-20 mm visibile in cima all’articolo), la cui parte più larga della testa -subito prima della punta- è più larga dell’asta (da 13-15 mm). Le frecce storiche potevano anche essere meno pesanti e meno larghe, 16 mm circa per quelle pesanti (con 20 mm immagino sia una bodkin pesante da 4-4,5 once), per cui l’energia necessaria per la completa penetrazione di 4 cm potrebbe essere meno grande di quanto stimato qui. Una via di mezzo, immagino, calcolata però solo sull’energia necessaria ad allargare il foro, non su quella per iniziare la frattura.
Prendo un esempio di Williams: contro il foglio da 1,9 mm di acciaio svedese di pessima qualità (W 0,6 circa), la punta di freccia da 40 gradi ha impiegato 80 J per causare un buco da 5 mm di diametro, mentre quella da 18 gradi 75 J. Non è una gran differenza. La differenza tra una freccia con la punta da 18 gradi e una con la punta da 40 è che magari la prima sarà larga quanto l’asta o meno (13-14 mm) mentre la seconda di più (16-20 mm) e quindi la seconda necessiterà di più energia per affondare la testa completamente. La seconda magari sarà una freccia pesante adatta per sfruttare al meglio gli archi potenti, 4-4,5 once per un arco da 150 libbre, mentre la prima sarà una freccia più leggera, 2-3 once, per i primi tiri a lunga distanza.
A occhio la mia stima è che se per iniziare la frattura servono 80 J a una e 75 J all’altra (W 0,6: immagino allora servano 130 J e 120 J contro dell’acciaio AISI 1010-1020) e per completare il buco da 40 mm servono 175 J, allora la bodkin aguzza da 18 gradi dovrebbe richiedere circa la metà dell’energia dell’altra per completare la penetrazione più l’energia per iniziarla: 140-145 J.
Anche una maglia di ferro è stata testata contro le frecce. Si tratta di un pezzo originale del XV secolo, 4-in-1, in acciaio a basso contenuto di carbonio indurito tramite tempra (forse 200 KJ/m2, ma con pezzi così piccoli non è possibile calcolare la tenacità), poggiato sopra una imbottitura di ben 26 strati (o forse 32, visto che a 180 J dice di averne passati 26 con la lama da 4 cm, nel test della alabarda contro maglia di ferro, mentre pone il superamento per intero a 200 J) di lino (un “jack” bello pesante).
La punta di freccia in questo caso è indicata come una punta bodkin da 18 gradi (non penso sia una bodkin ad ago, credo sia solo una bodkin da sfondamento molto aguzza), quindi più aguzza delle punte da 40 gradi precedenti. La freccia con 120 J ha spezzato due anelli e ha penetrato completamente l’imbottitura (circa 80 J per spezzare gli anelli, 20 J per perforare il jack pesante e altri 20 J per causare 35 mm di ammaccatura nella plastilina sottostante).
La buff coat (protezione in cuoio spessa 5 mm) è stata perforata con 30 J. Del corno di spessore non specificato è stato penetrato con 50 J.
I test coi proiettili
I test sono stati condotti utilizzando proiettili sferici simulati in acciaio. Le simulazioni con proiettili sferici in piombo morbido non sono ancora state studiate a fondo data l’enorme complessità che la deformazione “dinamica” del proiettile aggiunge. In un esempio della differenza tra proiettili in acciaio (pressoché indeformabile) e in piombo (deformabile) si è notato che se per causare una frattura in un foglio di metallo sono necessari 900 J con il proiettile di acciaio allora servono 1500 J con quello in piombo (+66%). Ma questo non è coerente con lo studio della differenza tra proiettili blindati e tondi in piombo fatto sulla formula di Krupp, che prevede una differenza di penetrazione di solo 20% (+34% energia cinetica). I valori forniti da Williams sono però abbastanza validi, dato che sono coerenti con altri test in cui erano stati utilizzati proiettili di piombo di calibro 16-18 mm.
I proiettili sferici hanno un comportamento diverso da quello delle frecce e l’energia necessaria per penetrare piastre sempre più spesse cresce, grossomodo, secondo una potenza di 2,2 (si veda la tabella). Questa però è una considerazione non completamente esatta. È valida solo se si vuole modellare l’ambito 1-3 mm come ha fatto Williams. In realtà, se si riconduce il tutto a formule più generali (come Krupp) si vedrà che i dati sotto i tre mm in questo caso si riconducono a livello più o meno grave all’ambito delle lamine sottili e non alla formula generale valida per spessori maggiori a causa della grande dimensione della sfera usata nei test (20mm in acciaio) rispetto allo spessore del foglio. Ci tornerò in futuro.
Comunque, in questo caso, i dati estrapolati da Williams sono sufficienti per il nostro ragionamento.
La tabella considera “sconfitta” l’armatura se il proiettile vi forma un buco largo quanto il proiettile stesso.
Tabella di Resistenza ai Proiettili
1 mm 2 mm 3 mm 4 mm Normale 155 J 750 J 1700 J 3400 J Impatto 30° 186 J 900 J 2000 J 4000 J Impatto 45° 217 J 1050 J 2300 J 4700 J
L’energia fornita dalle armi da fuoco è molto variabile, ma possiamo considerare questa guida divisa per periodo:
XIV secolo, prime armi da fuoco, 250 J; XV secolo, cannoni maneschi Hussiti (delle rozze bocche da fuoco in cui la carica veniva accesa con un ferro caldo), 500-1000 J; fine XV secolo – inizio XVI secolo, archibugi a miccia, 1300 J (polvere fine) o 1750 J (polvere in grani); dopo il 1525, moschetti di grosse dimensioni con forcella di supporto, 2300 J (polvere fine) o 3000 J (polvere in grani).
Per l’energia cinetica fornita dalle varie armi ad avancarica vi ricordo che c’è anche questo link.
Prendiamo in esame alcuni dei più famosi test realizzati in Austria (Krenn, 1990).
Sappiamo che un moschetto da 4444 J alla bocca ha penetrato completamente un foglio di acciaio morbido da 2 mm a 100 metri scagliandogli contro un proiettile di piombo di 38 grammi (calibro 19 mm). A quella distanza l’energia residua era probabilmente ridotta a metà o un terzo di quella originale, quindi circa 1800 J. Secondo la tabella è una cosa possibile, anzi, abbiamo perfino energia sovrabbondante!
Test condotto su un blocco di sapone con una pistola (14 grammi di proiettile, 1071 J alla bocca) e un moschetto (27 grammi, 2767 J alla bocca): la pistola a nove metri di distanza ha causato nel sapone una cavità di 23 centimetri cubi; il moschetto alla stessa distanza ha perforato un foglio in acciaio spesso 3 mm (con 300 VHP, equivalente a un’armatura di qualità III al massimo) e ha scavato una cavità di 25 centimetri cubi nel sapone, praticamente identica a quella della pistola.
Considerando che per scavare nel sapone un buco poco superiore (25 contro 23 cm cubi) l’energia necessaria è stata in proporzione poco maggiore a quella data dalla pistola, per semplice sottrazione possiamo notare che il proiettile di piombo (diametro 16,5 mm) ha impiegato 1600 J per forare l’acciaio il che è coerente con quanto ci attendevamo, considerando il calibro minore rispetto ai 18 mm possibili dei moschetti di grosso calibro per cui quella tabella è stata ottimizzata (dovendo agire come “generica”).
Un ulteriore test allo scopo di farsi un’idea più chiara di come la diminuzione del calibro diminuisca l’energia richiesta per perforare le armature: una pistola del XVI secolo ha sparato un proiettile (9,54 grammi, 11,7 mm, 907 J al momento dell’impatto) che ha penetrato una corazza del XVI secolo spessa 3 mm (300 VHP, identica al foglio usato prima) e si è fermato adagiandosi contro i due strati di lino posti sotto la corazza, a contatto con il sacco che faceva da supporto.
La palla da 16,5 mm ha penetrato l’acciaio con 1600 J (stimati!) e quella da 11,7 mm con 900 J. Poco più di metà dell’energia e se si guarda il rapporto tra le aree superficiali delle due sfere si vede infatti che la maggiore è due volte più grande della minore (in realtà, dalla formula, la differenza di dimensioni conta solo in parte ed entra in gioco anche il rapporto tra spessore della corazza e calibro del moschetto, maggiore di quello tra corazza e pistola, come accennato prima con Krupp). I conti sembrano tornare, grossomodo.
Si tratta comunque di stime, per quanto plausibili. Gli unici dati certi rimangono solo quelli dei test effettuati realmente con il moschetto e la pistola.
I test con lame e lance
Un uomo armato di lancia, spada o ascia può fornire qualcosa tra i 60-130 J. Un uomo molto forte con un’ascia o una spada impugnata a due mani può probabilmente arrivare a 200 J o oltre, come anche un uomo armato di alabarda.
Lama di 4 cm.
Con un impatto di 180 J la lama di 4 cm ha sconfitto la maglia di ferro del XV secolo: due anelli spezzati, due aperti, cinque piegati e l’imbottitura completamente penetrata. In particolare gli strati di lino sono stati penetrati in questa sequenza: 100 J (quinto strato), 120 J (nono), 140 J (sedicesimo), 160 J (ventitreesismo), 180 J (superato il ventiseisimo). La maglia di ferro di per sé ha offerto una resistenza di 80 J e l’imbottitura altri 100 J circa. Aggiungendo un po’ di energia per fare male al bersaglio sottostante, possiamo dedurre che servano più di 200 J per ferire un uomo coperto da un usbergo di maglia di ferro.
Questo con una lama di 4 cm, che può simulare le lame a mezzaluna di certe alabarde, ma se consideriamo che l’impatto reale di una spada può arrivare a coinvolgere 10 o più centimetri si può dedurre che sfondare una cotta di maglia usando la spada è fuori questione.
Per penetrare un foglio di ferro svedese di 1,9 mm (170 KJ/m2, W = 0,55 o forse 0,6 a causa dell’alta percentuale di scorie) la lama ha richiesto più di 190 J.
Altri test: la buff coat (in cuoio, 5 mm di spessore) è stata tagliata con 70 J; il corno (spessore non noto) è stato rotto con 120 J; il cuoio indurito nell’olio (spesso 5 mm) è stato tagliato con 90 J; l’imbottitura tipica che si indossa sotto le armature a piastre (16 strati di lino) è stata tagliata con 80 J.
Lancia.
Una lancia con la punta di 60° gradi ha richiesto 140 J per sconfiggere la maglia di ferro: tre anelli spezzati, due aperti, uno piegato e l’imbottitura completamente penetrata. L’imbottitura in questo caso si è comportata meno bene di prima, data la superficie di impatto più ridotta, offrendo probabilmente 70 J al massimo.
Contro il ferro svedese visto precedentemente la lancia ha richiesto più di 100 J per penetrare.
Altri test: il cuoio indurito nell’olio (spesso 5 mm) è stato perforato con 30 J; l’imbottitura tipica che si indossa sotto le armature a piastre (16 strati di lino) è stata penetrata con 50 J.
Conclusioni divise per periodo storico
Applichiamo quanto abbiamo visto e vediamo se è coerente con quanto storicamente è accaduto nel campo delle armature.
XI-XII Secolo.
L’armatura del cavaliere di quest’epoca è la cotta di maglia. Un’arma con lama richiederà più di 200 J per perforare la maglia: solo un uomo molto forte armato con un’ascia a due mani dalla lama piuttosto piccola (come l’ascia danese lunga 1,2-1,5 metri) può sperare di farcela. Però una freccia richiede solo 120 J per conficcarsi a fondo nel bersaglio, il che è nelle possibilità di un arco lungo da 150 libbre a distanza ravvicinata o di una balestra non molto potente.
I colpi di spada, mazza e ascia potrebbero riempire di lividi o anche spezzare le ossa del cavaliere, ma non subirà tagli, amputazioni immediate o ferite aperte estese. I medici medievali sapevano trattare benissimo le fratture, ma nei confronti delle ferite infette erano pressoché impotenti: la cotta di maglia non si limitava a offrire una buona protezione, ma evitava che la morte sopraggiungesse successivamente a causa dei batteri entrati nelle ferite da taglio.
Le frecce provenienti da distanze medio-lunghe si conficcheranno nella cotta di maglia o verrano deviate, creando quell’immagine del cavaliere puntaspilli (ma illeso!) che i narratori medievali hanno tramandato.
XIII-XIV Secolo.
Il cavaliere deve rinforzare la propria armatura per resistere al crescente pericolo determinato dalle balestre. Aggiungendo sopra la maglia di ferro una cotta di piastre spessa 2 mm, in ferro da munizione (qualità I), può aumentare di 70 J circa la resistenza contro le frecce e i dardi. Una freccia avrà bisogno di 200 J per infliggergli una ferita, il che è completamente fuori dalle capacità dell’arco lungo, ma può essere ancora possibile con un colpo a bruciapelo delle balestre da guerra più pesanti (200-250 J, per balestre da 1200-2000 libbre caricate con martinetti o sistemi a carrucola).
Ulteriori rinforzi sotto forma di piastre per braccia e stinchi in cuoio indurito, bronzo o ferro andranno a formare quell’armatura in maglia e piastre metalliche del Trecento, periodo di transizione tra l’usbergo e l’armatura bianca.
 |
| Cavalieri del Trecento: Italia Centrale, Germania e Catalogna |
XV Secolo.
Un cavaliere equipaggiato con la protezione migliore disponibile indosserà un’armatura milanese, spessa 2 mm, arrotondata e fatta con acciaio a contenuto medio di carbonio (consideriamo qualità III, ma potrebbe essere anche stata indurita fino a qualità IV).
Una freccia avrà bisogno di 230 J per penetrarla e altri 50 J per superare l’imbottitura sottostante e causare una ferita: 280 J sono fuori dalle possibilità perfino delle balestre con archi in acciaio. L’armaiolo può dichiarare senza problemi che questa armatura è “a prova di balestra”. Un proiettile di grosso calibro avrà bisogno di quasi 1000 J per penetrarla, il che è nel limite dei cannoni maneschi più potenti usati dagli Hussiti. Il cavaliere è salvo, ma per poco.
Se la sua armatura fosse stata fabbricata nel Nord Europa, con acciai peggiori (qualità II), la protezione contro i proiettili sarebbe di circa 700 J il che lo metterebbe in pericolo nel caso dovesse incontrare cannoni maneschi a distanza ravvicinata. Un problema compatibile con quelli avuti dai cavalieri tedeschi nel corso della repressione dell’eresia Hussita sostenuta dal movimento taborita (1420-1434).
XVI Secolo.
Un lanzichenecco o un picchiere svizzero indosserà probabilmente una corazza di Norimberga (acciaio di qualità II), spessa 2,5 mm e di forma spigolata. Una freccia colpendo a 45° avrà bisogno di 260 J per penetrare (310 J se è presente una imbottitura, cosa che dalle immagini dell’epoca pare non fosse molto comune…) il che è fuori dalle capacità perfino delle balestre. Un proiettile d’altro canto avrà bisogno di solo 1250 J, il che è perfettamente nelle possibilità di un archibugio a breve distanza.
Un cavaliere con indosso un’armatura spigolata di produzione milanese (qualità III), spessa 3 mm, potrà resistere a proiettili fino a 2500 J. Gli archibugi e i caliver non potranno minacciarlo, ma un pesante moschetto con la forcella caricato con polvere in grani potrà offrire 3000 J a distanza ravvicinata.
Questo è coerente con le riforme dell’epoca (il tercio spagnolo di Spinola, ad esempio, o le innovazioni olandesi di Maurizio d’Orange) per cui vennero inseriti nei battaglioni di fanteria un certo numero di tiratori armati di moschetti di grosso calibro, pesanti anche 9 kg l’uno, e sostenuti in posizione di tiro grazie a una lunga forcella.
 |
| Moschettiere di fine XVI secolo / prima metà del XVII secolo |
XVII Secolo.
Un’armatura a tre-quarti da corazziere sarà arrotondata, spessa 4 mm e fatta in ferraccio da munizione (qualità I). Un proiettile avrà bisogno di 2000 J per sfondarla, il che è al di là delle possibilità di una pistola (anche a bruciapelo) o di un archibugio leggero, ma è nelle possibilità di un moschetto pesante con la forcella. Questo genere di armatura, prodotta in massa per armare cavalieri temibili come i corazzieri livoniani di Gustavo Adolfo o simili, è molto pesante a causa del grande spessore e può arrivare anche a 40 kg (89 libbre in un esemplare storico realizzato per un uomo decisamente robusto): decisamente troppo per un soldato appiedato!
 |
| Un Ironside parlamentare (in corazza, elmetto e buff coat) fa un regalo a un Corazziere realista (in armatura a tre-quarti) |
Lieto Fine (?)
L’effettiva evoluzione delle armature sembra essere stata rispettata dai modelli che abbiamo considerato. Le armi da fuoco hanno portato a una corsa prima alla qualità degli acciai e poi allo spessore della armature, anche a scapito della qualità. Rendere l’armatura spessa il doppio costa molto meno che impiegare un acciaio tre o quattro volte migliore e una corazza in ferraccio da 4 mm prodotta in massa è solida quanto una corazza di 2 mm forgiata nel migliore acciaio indurito dai maestri armaioli di Greenwich.

dico solo una cosa: sei un mito.
fichissimo. i tuoi articoli sono stati interessanti, e se mai dovessi scrivere qualcosa tornerò di sicuro a rileggerli. grazie mille.
ehm, approfitto della tua preparazione e disponibilità per una domanda che ti farà rizzare i capelli in testa per la sua idiozia, ma io davvero non so rispondermi: ma un colpo a bruciapelo di arco (diciamo, sotto il mezzo metro) esprime la sua massima forza possibile? mi spiego: ho sempre pensato che parte della forza di una freccia dipendesse dall’energia cinetica accumulata nel percorso. ora, questa in parte è quasi di sicuro una cazzata (forse in contrasto con parte della fisica, almeno per i tiri in cui destinatario e il mittente sono grosso modo alla stessa altezza), però una conferma netta potrebbe essere interessante.
grazie ancora,
mhrrr
Non ti preoccupare: nessuna domanda è stupida se chi la pone è realmente interessato alla risposta. Il problema di solito è trovare le risposte, ma in questo caso sono stato fortunato e non mi hai chiesto nulla di “terribile”. :-)
Colpo a bruciapelo. Ipotizziamo che l’arco sia distante dal bersaglio un metro circa, giusto per fare in modo che la freccia lunga 28-32 pollici circa (70-80 cm) abbia abbandonato l’arco ricevendone tutta la spinta che questo poteva dargli.
Avrà l’energia massima possibile, ovvero circa 130 J per un arco da 150 libbre che scaglia una freccia pesante poco meno di un etto.
Essendo appena partita non dovrebbe star scodando troppo, per cui possiamo ipotizzare che voli ancora “dritta” e possa colpire al meglio il bersaglio …se poi il bersaglio stesso è sagomato -arrotondato o spigolato-, amen: almeno non si peggiora troppo la situazione!
Non ho idea se “scodare” sia un termine accettabile: ho sempre letto e sentito questo, ma magari c’è un termine tecnico specifico che ignoro…
Se invece consideriamo la freccia nei primi 10 metri di volo (o anche più, non so darti una stima esatta) la troveremo che sta scodando pesantemente muovendo testa e culo per fare quel movimento “da serpente/onda” che compiono le frecce per acquistare una traiettoria stabile.
Un’asta in rigido metallo renderebbe la freccia meno precisa oltre a rovinare il punto di baricentro e rendere meno buona la penetrazione, che è favorita dalla “testa pesante” rispetto all’asta. Pensa ai dardi/quadrelli di balestra: corti, tozzi, con teste molto pesanti che concentrano la massa vicino al punto di impatto.
Le frecce migliori compiono questo movimento solo nell’asta, mantenendo miracolosamente immobili testa e culo. Se cerchi video con i super-atleti coreani certe volte si vedono le frecce al rallentatore e puoi goderti il loro scodare.
Comunque se parliamo di frecce normali, entro i primi 10-20 metri dovrebbero avere la testa molto instabile per cui si rischia di colpire con un cattivo angolo un bersaglio anche se si è tirato con un’allineamento perfettamente a perpendicolo.
L’energia cinetica non viene acquisita viaggiando, perlomeno non nella prima fase del volo. Inizialmente la freccia viene guidata in avanti con una componente Vx e in alto con una Vy: Vx viene contrastata dalla densità dell’aria attraversata (circa 1/1000 di quella dell’acqua) e Vy viene contrastata sia dall’aria che dalla forza di gravità.
Quando Vy si annulla la freccia ha raggiunto l’apice verticale della traiettoria e comincia a cadere, acquistando una velocità verticale sempre maggiore grazie alla forza di gravità. Suppongo fosse quello che intendevi dicendo “accumula energia cinetica”.
Questo spiega perché le frecce al termine del viaggio non hanno un’energia cinetica così drasticamente diversa da quando erano partite: da 111 J a 64 J dopo 330 yarde.
Magari parlerò meglio di queste cose quando dedicherò un articolo agli archi da guerra medievali.
Spero di esserti stato di aiuto.
:-)
mi sei stato di grande aiuto e aspetto il tuo articolo sugli archi con curiosità. ti ringrazio ancora per la completezza della risposta; farò tesoro di tutte queste informazioni.
ah, e OT mi permetto di esprimere il mio totale accordo con quanto detto sui gdr.
a presto.
Grazie a te per essere tornato a leggere Baionette Librarie. :-)
Se conosci qualche escort-cosplayer-elfa come nell’annuncio che ho messo, fammi sapere!
:-P
Praticamente le migliori informazioni a riguardo (almeno in italiano) che ho trovato sul web.
Complete di sperimentazioni, consulenze e citazione delle fonti piu’ importanti.
In pratica e’ quasi un breve saggio storico/fisico.
Complimenti vivissimi.
Da adesso sei il mio punto di riferimento per le informazioni di questo tipo.
Grazie per l’apprezzamento.
Sempre sull’argomento “corazze” ho del materiale informativo extra per un breve articolo dedicato sia alle corazze duplex che ai Marchi di Prova sulle armature dei corazzieri che venivano garantite a prova di pistola o di moschetto.
:-)
Mi sono imbattuto casualmente in questo sito e sono stato fortunato poichè lo studio balistico sulla resistenza delle corazze è ottimo, sinceramente.Fra l’altro conferma la mia convinzione che se le armature erano usate a qualcosa servivano. Crecy, Azincourt, archi parti o mongoli e così via: si leggono un sacco di fesserie sulla presunta forza, contro le corazze, di queste armi (ovviamente in base all’evoluzione oplologica). Personalmente ho fatto un test (prossimamente visibile in una serie di documentari televisivi sul Medioevo)usando una piastra di 1 m. x 1 m di ferro acciaioso di 1,5 mm. Essendo piatta non defletteva le frecce e quindi l’impatto e prendeva il colpo in pieno, nel contempo però la vibrazione causata dal colpo lo ammortizzava. I tiri da 30 m., più volte ripetuti, hanno dato questi risultati: freccia sfondagiaco lanciata da arco italiano da 60 lb., nessuna perforazione; stesse frecce con arco composito 60 lb., idem; arco longbow da 100 lb.,perforazione con fuoriuscita di circa 3 millimetri; balestra con arco in legno di circa 90 lb, nessuna perforazione;balestra con arco in acciaio da 150 lb., perforazione di circa 4 mm.; balestra pesante da 250 lb., perforazione di 5 mm.In pratica (considerando anche la sottostante imbottitura) nessuna ferita grave. In pratica, i famosi archi inglesi vinsero i francesi solo per la loro stupidità e per il fatto di averli privati delle cavalcature non protette. Quasi immobilizzati, finirono quasi tutti sgozzati e ammazzati a colpa di mazza.Per quanto riguarda i mongoli, gli effetti venivano ottenuti a causa della perdita di sangue causata da molteplici ferite non gravi e infine dalla spossatezza (senza poter arrivare a contatto con loro). Saluti.
Ottimo, grazie per i dati in più, Giovanni!
Se li hai ancora disponibili mi potresti fornire peso e velocità delle frecce utilizzate? In particolare mi interessa il peso.
Avevano la forma compatta e la struttura in acciaio indurito, da sfondamento, come l’esemplare B o molto simili?
Non sono mai sazio di informazioni extra! :-P
Ciao e grazie per essere venuto! ^__^
Un’altro articolo molto bello, ben documentato, di facile lettura e completo dei minimi dettagli. Raramente in rete si trovano informazioni cosi’ ordinate su questi temi, sopratutto in italiano. Mi sono letto tutti gli articoli piu’ volte, una vera fortuna aver trovato questo sito.
Complimenti vivissimi e grazie per il tempo dedicato a scrivere questi articoli.
prima di tutto ti faccio saoere che il tuo blog è infetto de malware rompicazzi
grande l’articolo
un pò non mi trovo con la tua fede nell’ipertrofia ma sono daccordo con te al 95%
solo che l’iperlordosi dell’arcere massiccio del video è inefficente sia in termini di qualià del tiro che in efficenza meccanica
insomma mi sembra che si trascuri un po la tecnica aretstica
Ciao, ho appena letto un po’ dei tuoi articoli e devo dire che sono davvero interessanti e completi, quindi complimenti.
Avrei da farti delle domande per soddisfare la mia curiosità:
1. qual era la causa più frequente di morte per un soldato pesantemente corazzato? cioè mi pare di capire che nel XVII secolo le armature rendevano praticamente invulnerabile il soldato, tranne contro i cannoni e i moschetti pesanti.
2. come venivano neutralizzati (se era possibile) questi soldati senza armi da fuoco?
3. se si dovesse fare una battaglia senza armi da fuoco tra un esercito pesantemente corazzato contro una legione romana o le armate macedoni di Alessandro Magno chi risulterebbe più avvantagiato, o meglio: su chi scommetteresti?
Forse sono domande un po’ scocche di chi non conosce bene l’argomento, scusa per il disturdo.
1. A Wisby, dove già le armature lamellari e le cotte di piastre erano in grado di fermare le armi bianche, le ferite sono principalmente al volto e agli arti. Più i traumi cranici a gente senza elmo o con protezioni leggere.
2. Colpendo dove non c’è l’armatura (quando possibile: l’armatura da fante di Enrico VIII era priva di qualsiasi punto debole, ma è una caso eccezionale e non la regola): faccia, retro delle cosce, genitali sotto il gonnellino in maglia di ferro, apertura della corazza sotto le ascelle… bersagli piccoli e difficili, ma non c’è molta scelta.
Se l’elmo è chiuso e il resto non è accessibile si può lottare per alzare la celata, poi infilzare il volto e pestarlo col manico della “misericordia” (un nome dei pugnali dell’epoca).
3. Dipende.
Ipotizziamo che sia una fanteria del ‘500-‘600, coi picchieri dotati di corazze petto-e-schiena ed elmetti, ma non di protezioni per braccia e gambe. E che la cavalleria di appoggio sia formata da cavalleria pesante alla svedese o corazzieri senza pistole, con spade e lance, protetta con armature a tre quarti e stivali lunghi o buff coat, stivali lunghi e corazza.
E ipotizziamo che il numero di fanti e di cavalieri sia uguale per ambo gli schieramenti.
3a. Contro i macedoni, in cui i fanti con la sarissa sono il rullo compressore, ma la cavalleria è ciò che “vince la battaglia” credo vincerebbero quelli del ‘600 anche senza armi da fuoco. Le corazzature sono superiori sia in fanteria che in cavalleria (ma già il lino pressato e il bronzo dei fanti macedoni è sufficiente a fermare le punte di picca) e i fanti in formazioni chiusa contrapponendo picche a picche si potrebbero scannare alla pari, ma nella cavalleria il divario è enormemente a vantaggio dei ‘600eschi: mentre i nemici hanno perlopiù braccia e gambe scoperti, loro sono completamente invulnerabili tra cuoio indurito e acciaio indossato ovunque.
E staffe per tenerli ben in sella durante una carica di lancia o di spada, bella violenta, gettandosi con tutto il peso dei cavalli e delle armature.
E selle pesanti adatte al combattimento, tecnologicamente superiori a quelle nemiche.
3b. Contro legionari romani del tempo di Giulio Cesare, con cotte di maglia, scudi, giavellotti e gladi, i romani avrebbero lo svantaggio delle cotte di maglia senza imbottitura “spessa” (che le picche possono far cedere con colpi abbastanza violenti, incrinando costole), ma anche l’enorme vantaggio degli scudi.
La cavalleria romana, come nel caso dei macedoni, verrebbe spazzata via dalla massa di acciaio della cavalleria moderna in armatura.
Se i picchieri riusciranno ad evitare che si entri in un corpo a corpo e tengono le distanze usando le picche potranno essere certi della vittoria non appena i corazzieri si saranno liberati dei nemici e investiranno come un treno il fianco dei romani, costringendoli a subire l’impatto di una carica a fondo del genere che già i Parti avevano dimostrato efficacissima contro i legionari, capace di scavare per metri dentro lo schieramento.
E a parte i cavalli e le giunture questi cavalieri sarebbero immuni alle spade romane, che colpivano sia di punta che di taglio (fonti storiche riportano arti mozzati sui campi di battaglia).
Direi che anche in questo caso il più “invulnerabile” è avvantaggiato.
Non è il genere di domande a cui posso dare risposte sicure, ma sono comunque spunti di discussione interessanti.
Davvero ben fatto, solo magari mi aspettavo ti soffermassi più sul periodo medievale. se uscirà qualcosa di nuovo, se possibile mi piacerebbe esserne informata, senza recare disturbo (qualcos’ altro sul medioevo) complimenti davvero, molto esauriente
Questo lo hai letto?
https://www.steamfantasy.it/blog/2008/10/20/performance-arco-da-guerra-inglese/
Penso che potrebbe interessarti.
Era tantissimo tempo che cercavo queste informazioni riguardo resistenza di armature ed efficacia, dato che ho una discreta passione per armi e armature stesse.
Grazie molte… sei appena diventato l’ eroe di un 18enne XD
Ciao e continua così
anche io ti faccio una domanda idiota!
Qual’è l’efficacia di una katana contro un’armatura in metallo? in particolare contro un’armatura europea (adesso van di moda i samurai e tutti a dire che un samura avrebbe la meglio contro un contemporaneo europeo… sinceramente non scommetterei un centesimo sul samurai)
Puoi applicare pari pari il caso della lama di 4 cm perché si tratterebbe di acciaio più duro (filo in martensite e struttura a strati sempre meno dura e più elastica per dissipare gli stress da impatto senza rompersi) contro acciaio meno duro. Quindi nessuna possibilità di eccessiva spinta che può portare a deformazione dell’attaccante (come potrebbe essere per un proiettile di piombo morbido quando l’ostacolo oppone troppa resistenza causando una decelerazione altissima).
Se la katana è leggermente curva, come capita spesso, puoi aggiungere al conto una predisposizione al colpo angolato (per favorire il taglio della carne, sul modello della sciabola curva) che rende meno valido lo scarico della forza.
Come una normale spada non taglia una corazza appena decente. O anche solo una cotta di maglia: immaginiamo 4 cm di taglio sull’avambraccio, richiede tra maglia e imbottiture 180 J o poco meno! Una persona ne farà un 60-130, forse uno massiccio e molto bravo nell’imporre massa del corpo dietro il colpo e a dare velocità alla lama può arrivare oltre i 150J… decisamente una bella botta sul braccio (magari lo spezza anche), ma non passa tutta la protezione di tessuto imbottito sotto la maglia spezzata. O se la passa la passa di poco (immaginiamo un samurai in grado di dare colpi di spada forti come colpi di alabarda nonostante la massa molto inferiore: 200 J).
E se già pensiamo a un colpo di 8-10 cm sul torso servono forse erculee (350-400 J?) per tagliare tutta quella roba: bisogna accontentarsi dei lividi e delle botte per poi andare di punta o di taglio sui punti senza armatura…
Con la lama molto affilata (minore superficie di impatto) e molto dura (più dura della tipica armatura incontrata) si può ottenere uno straordinario taglio in tessuti molli come la carne, ma dubito che sia molto vantaggioso contro un’armatura: anche se inizi più facilmente il “graffio”, dopo la lama aumenta di spessore per aumentare anche di massa e quindi devi aumentare anche la “dimensione del taglio per passare” fino a livelli da spada europea (e se non lo fa allora ha lo svantaggio di pesare poco, quindi la minore energia cinetica richiesta per tagliare è bilanciata dalla penalità in termini di energia fornita all’impatto… il peso nel taglio è determinante per sfondare e l’acciaio pesa uguale in una spada europea e in una katana).
Contro un’armatura milanese la katana si spezzerebbe al secondo colpo sferrato a tutta forza. Non a caso, la spada europea, per far fronte alle protezioni sempre migliori, subì una evoluzione verso il colpo di punta, da portare con tecniche di mezza spada, e verso il danno da botta (una zweihander da 3,5 kg maneggiata da un bestione poteva rompere un braccio).
Complimenti. Ho trovato i dati da Lei esposti molto interessanti. Ho confrontato alcuni dati con Williams e li ho trovati corrispondenti. Dopo i complimenti, volevo dirle che sarebbe stato molto più apprezzato, perchè citabile, se a riferimenti specifici, seguissero, fonte e pagina, con una distinzione tra dati presi dalle fonti autorevoli da Lei citate ed invece quanto è una sua opinione, rispettabilissima, per carità, ma vedo questo il modo di scrivere di molti autori, le note sono sempre esposte con piccoli numeri… Mi riferisco in particolare agli altri testi da lei citati. Le dico questo perchè ho usato quanto da Lei detto in un forum, mi è stato chiesto di citare fonte, autore e pagina…Il Duca Carraronan in questo link cita queste fonti con questo autore a questa pagina…ma così non posso sapere quello che Lei afferma da quale libro è stato preso. Non la prenda come una critica, ma come un invito a rendere il suo lodevole lavoro più facilmente portabile a riprova di quanto si afferma.
Un altra cosa, una spada da spinta, quindi con una superficie molto piccola, assimilabile ad una freccia, non viene affatto menzionata…quanti Joule può svillupare? può forare un cosciale da 1.5 mm di acciaio di grado I? Ecco il suo articolo lo trovo in linea con le mie informazioni, ma manca di questo. Se vorrà ampliarlo, forse l’annosa questione circa la resistenza delle armature potrà aver fine.
Se prende quanto da me detto come una critica costruttiva, me sarei davvero felice. Il suo è un ottimo lavoro, penso di sapere un pochino di armi, e Lei è molto competente. Di nuovo complimenti.
Sì, vero. I libri utilizzati sono quelli indicati in alto, però mancano i riferimenti alle pagine o perlomeno al capitolo (per quello di Hall è tutto nello stesso capitolo). All’epoca non curavo granché la bibliografia degli articoli, citavo giusto il titolo dei libri e nemmeno in modo ordinato in fondo al testo. Invece nell’articolo sulle Popoffka, a dicembre, ad esempio ho segnato di ogni libro le pagine esatte usate.
Appena ho tempo cerco di recuperare i numeri delle pagine.
Un superficie così piccola e aguzza da sembrare una freccia da sfondamento, come, uh, un Estoc?
In tal caso credo si possa stimare che l’energia necessaria per penetrare di 40 mm sia la stessa che per le frecce da sfondamento: 55 J (40 J per iniziare a penetrare). Va poi considerato se il cosciale è arrotondato o spigolato (o se magari è arrotondato, ma l’impatto arriva a 90 gradi è come se non lo fosse)
Williams per lance, asce, spade ecc… stimava da un uomo normale (non un bestione) energie di 60-130 J. Direi quindi che sembrerebbe fattibile.
Se invece la punta diventa rapidamente è più larga, somigliando più a quella di una lancia… eh, bella domanda. Per la lancia abbiamo solo i 100 J sul ferraccio svedese da 1,9 mm (puoi conteggiarlo come poco meglio di “grado I”). Non c’è molto materiale per poter far stime. Si rientra sempre negli sfondamenti “normali”, con l’apertura del metallo e il passaggio attraverso del corpo, senza l’asportazione di un pezzo del metallo (il proiettile a punta tondeggiante, ad esempio, ha quel modo strano di calcolare l’energia necessaria all’aumentare del diametro nella formula di Krupp perché taglia un disco di metallo e se lo porta via… per questo non è direttamente proporzionale alla superficie, ma è più legata alla circonferenza).
A occhio immagino 65-70 J per iniziare a bucare, di più per penetrare di 40 mm… se alla fine la lama penetra bene, mettiamo fino a dove si allarga a 3 cm, possiamo stimare 3/4 dell’energia necessaria per una lama da 4 cm… 100 J circa. Sempre senza considerare il design della piastra.
Ma davvero non saprei: troppi pochi dati disponibili per le lame e le punte di lancia.
In che forum c’è stata la discussione?
Chiedo un chiarimento sulle dinamiche di una ipotetica battaglia del ‘600 in cui erano schierati picchieri, fanteria pesante armata di alabarde o spadoni, Moschettieri e pistolieri di cavalleria. (tutti per entrambe le fazioni).
1- Vorrei capire se il fulcro della battaglia era nel combattimento a distanza medio-lunga con armi da fuoco o a distanza ravvicinata con picche e armi da mischia.
Chiedo questo perche dal tuo articolo nn ho ben capito se la maggior parte delle morti avveniva negli scontri a fuoco o nel corpo a corpo.
2- Inoltre, perche i fanti nn portavano un’armatura completa ma soltanto una protezione petto-schiena e un elmo senza celata? non era necessario coprire gli arti in un quadrato di picchieri?
3- L’ultima domanda riguarda i cavalli. Essi erano dotati o meno di pettorale per la protezione dalle picche e dai proiettili, tenendo conto del fatto che il petto di un cavallo in carica rappresenta un bersaglio alquanto invitante per la linea di fuoco dei moschettieri? Se no, Perche?
grazie in anticipo per le tue risposte.
hai trovato le informazioni che ti avevo chiesto?
@luca
Non devo trovarle, le avevo già.
Il problema è che ci vuole tempo e voglia di rispondere, se si vuole rispondere motivando. E per ora non ho avuto tempo o voglia.
Se hai fretta puoi informarti da solo (io l’ho sempre fatto): resoconti e testi per rispondere alle tue domande non mancano, se si vuole cercare.
Inoltre noto che hai preferito usare i commenti di un articolo per domande tecniche solo vagamente correlate all’articolo, invece di mandare una mail… questo non mi rende particolarmente ben disposto.
Se e quando avrò voglia, ti scriverò una risposta.
Attendi.
ok, scusa per l’insistenza eh…
Domani scriverò la risposta.
Devo recuperare un altro esempio decente per la domanda uno. Se non faccio in tempo ne userò uno solo, quello già ripescato dalla fonte più comoda che ricordavo. Non mi piace molto il Seicento, ormai.
Risposta per luca.
Ti lascio questa risposta iniziale, un po’ breve, poi se in futuro avrò tempo la estenderò facendo un articolo a parte con più dati ed esempi. In questi giorni non ho proprio avuto tempo per darti la risposta articolata che ti volevo dare, mi spiace. :-(
L’evoluzione del rapporto tra picche e archibugi dalla fine del ‘500 alla metà del ‘600 ci dice che vengono ridotti sempre di più i picchieri e aumentati sempre di più gli archibugieri (sia pesanti, con forcella, che meno pesanti): si passa in poco tempo da 1 archibugiere ogni 2 picchieri a 3 archibugieri per ogni picchiere. E a fine ‘600 i picchieri spariscono proprio da gran parte degli eserciti.
Così, a intuito, secondo te chi dei due fa più vittime e influisce di più sulla vittoria in battaglia nel ‘600 (il secolo della pike-and-shot)?
^___^
Ora, con una semplificazione stupida, cerco di spiegare i pochi concetti cardine del pike-and-shot.
Gli archibugieri forniscono volume di fuoco in modo più agile dell’artiglieria, seppure a gittata inferiore. Gli archibugieri però sono indifesi contro la cavalleria, allora hanno bisogno dei picchieri con cui operano SEMPRE assieme.
La cavalleria è l’unica in grado di manovrare rapidamente, mentre i quadrati di fanteria sono lenti e pesanti. La cavalleria di conseguenza è l’unica che possa sperare di prendere di sorpresa gli archibugieri e, soprattutto, catturare i cannoni che dovessero trovarsi indifesi.
Non può però affrontare i picchieri, i cui quadrati sono invulnerabili (o quasi). E anche la semplice protezione degli archibugieri talvolta basta a frenare, tra morti e altro, le cariche di cavalleria impedendo la vittoria: fare il caracollo scaricando le pistole a turno contro la fanteria è un mezzo suicidio, perché i fanti con archibugio possono tirare in risposta meglio e con più rapidità.
I picchieri però sono tutti ammassati e sono altamente vulnerabili al fuoco. Vanno quindi scompigliati col fuoco di artiglieria e archibugieri, prima di poter pensare di caricarli con la cavalleria.
I picchieri non possono nemmeno avvicinarsi per affrontare il nemico: se si avvicinano il fuoco diventa più letale e loro devono avanzare in formazione, perché se si si scompaginano poi vengono falciati dalla cavalleria.
Devono sopportare a affidarsi ai propri archibugieri, gli unici in grado di rispondere al nemico. E in più se si muovono in fretta verso il nemico, gli archibugieri non possono usare il fuoco rapido su file: inizieranno a subire molto più fuoco di quanto ne possono dare in risposta!
Gli scontri si riducono a cariche di cavalleria inefficaci, seguite e precedute da lunghi periodi con i quadrati di picchieri immobili che subiscono il fuoco mentre i loro colleghi archibugieri rispondono.
Il ruolo dei picchieri non è tanto quello di “uccidere”, ma di proteggere evitando che i propri archibugieri vengano uccisi. Se i picchieri cedono sotto il fuoco o se non sono veloci ad affrontare la cavalleria in arrivo, è la fine: i cavalieri Sassoni a Breitenfeld fallirono il loro compito e solo grazie alla rapida reazione dei picchieri e dei moschettieri l’ala sinistra degli Svedesi non crollò sotto la carica della cavalleria Imperiale.
Sempre alla battaglia di Breitenfeld del 1631, l’ala sinistra Imperiale con l’ottima cavalleria di Pappenheim fece ben SETTE cariche contro l’ala destra svedese e venne ogni volta respinta e scacciata nel caos dal fuoco dei moschetti (gli svedesi avevano molti più archibugieri degli imperiali e meno picchieri -2 a 1-, oltre a un addestramento specifico al tiro rapido con l’uso di rapide cartucce di carta al posto delle bandoliere di cariche e dei proiettili sciolti).
Non c’è da stupirsi se si racconta che spesso alcuni picchieri abbandonavano la picca e prendevano gli archibugi dei morti, per non sentirsi solo come inutili bersagli del nemico.
Peso e costo, ma soprattutto il costo.
Le armature costano, molto, soprattutto quando entrano in gioco cinturini, rivetti ecc… per tenerle insieme e renderle indossabili (una corazza con spallacci venduta a 26 scellini poteva costare in produzione 13 scellini di cui 5,5 di corazza e 7,5 di cinturini e lavoretti per renderla indossabile, fonte “The armourer and his craft” di Ffoulkes, appendice J… con le armature da lancia, a 3/4, i costi salgono ancora i più).
Un corsaletto da fanteria, che protegge petto, pancia, schiena, collo, spalle e porzione superiore del braccio, e scende con i fiancali fino a metà coscia, nel 1590 costava 30 scellini.
Avambracci scoperti, interno del bicipite scoperto, metà coscia in giù scoperto… e manca al costo il morione o la borgognotta, che sono altri 3,3-4 scellini e la faccia rimane comunque scoperta (ma uno deve pur poter respirare bene a guardare quel che fa se lotta a piedi nella mischia, no?). 34 scellini e ancora è mezzo scoperto, con un sacco di punti per essere colpito dalle picche e dalla daghe.
E l’armatura non è nemmeno a prova di moschetto (in realtà nessuna lo è a bruciapelo, se non quelle da 6-8 mm, ma si intende “a prova di moschetto pesante oltre i 100 metri”) o di pistola: si sfonda senza problemi quando gli archibugieri fanno fuoco mentre il lento quadrato di picchieri avanza. Una corazza “a prova”, senza i mezzi cosciali e le spalle, verrebbe da solo 30-40 scellini.
Per renderlo a prova di archibugio, perlomeno dai 100 metri (limite in cui il fuoco nemico comincia a fare un po’ di danni interessanti), e ben coperto dal ginocchio alla cima della testa serve un’armatura da corazziere a 3/4. Ma pesa 40 kg e costa 80 scellini! E nelle ultime decine di metri verrà falciato dai proiettili esattamente come se indossasse solo una corazza petto-e-schiena da 20 scellini e 7-8 kg di peso. E la distanza sotto i 100 metri è quella che fa più vittime sempre quindi non si viene difesi nell’unico momento in cui l’armatura dovrebbe difenderli (considerando che il corpo a corpo puro tra quadrati di fanteria è solo l’ultima fase, se non si risolve col fuoco o la cavalleria il tutto).
Non mi pare intelligente vederlo morire allo stesso modo, spendendo 4 volte tanto in armatura, appesantendolo e stancandolo ancora di più (avvolto da 30 kg di acciaio in più, senza ventilazione nell’armatura, magari con il sole a picco in estate… durano parecchio nelle ore e ore di battaglia i picchieri, così messi!) e quindi rendendolo perfino meno efficiente… per cosa: per renderlo invulnerabile alle armi da corpo a corpo e ai moschetti sopra i 100 metri?
Per il resto i fanti non erano male equipaggiati per il corpo a corpo, per quanto ormai importasse sempre meno: corazza petto-e-schiena (certe volte con enormi e scomodi fiancali squadrati che proteggono fino a metà coscia), spesso buff coat di cuoio con o senza braccia (per proteggere collo e inguine dalle lame, perlomeno quando la corazza non ha i grandi fiancali: le buff coat sono ottime contro i colpi da taglio e frenano piuttosto bene anche le punte di lancia, perlomeno i colpi meno forti). Un buon compromesso tra il massimo del peso che erano disposti a sopportare e la protezione efficace (ricordiamoci che sono persone denutrite, basse di statura, stanche, indebolite, spesso malate a causa delle condizioni orrende della vita militare, costrette a lunghe e faticose marce… che non volessero tenersi addosso 20 kg di ferraglia ulteriore mi pare il minimo, no?).
Le fonti storiche (manuali militari dell’epoca, dipinti ecc…) dimostrano che non indossavano più protezioni, nemmeno quelli dei corazzieri in armatura a 3/4, e che già a inizio ‘500 i cavalli con armature non erano tutti.
La risposta è semplice: se già serviva un cavallo molto robusto per portare una sella pesante, un corazziere grande e grosso (80-100 kg di uomo?) con un’armatura grande e grossa (armatura da corazziere tipica a 3/4, spessa 4 e + millimetri, a prova di pistola: 40,5 Kg, contro i 25-30 Kg delle armature complete di un secolo prima), più armi (due o tre pistole, talvolta un archibugio, di solito una spada) e pure così l’animale era affaticato e rallentato dal peso… vuoi anche coprirlo con un’armatura?
Le armature per i cavalli spesso erano spesse solo 1/16 di pollice (1,5 mm, si immagina del miglior acciaio), buono per fermare lame, mazze e parecchie frecce… per fermare proiettili dovrebbero essere spesse 4 mm e oltre (6 mm per fermare i moschetti con la forcella a bruciapelo): cosa sono, altri 200 kg di metallo sul cavallo?
E’ follia immaginare che possano muoversi e combattere in quel modo. E d’altronde la principale minaccia sono le armi da fuoco, come spiegato prima. Proteggerli, appesantendoli parecchio (e quindi rallentandoli), anche solo contro le picche con un’armatura da 1,5 mm sarebbe follia: le armi bianche sono il male minore e costa troppo farlo (e comunque le zampe e il collo rimangono scoperti, permettendo lo stesso di uccidere il cavallo).
grazie, la tua risposta è stata esauriente anche cosi. se dovessi chiederti altre informazioni preferisci che le chieda qui o tramite e-mail?
Se non sono direttamente correlate all’argomento del post, preferisco le mail. Ne ricevo almeno una ogni due giorni e cerco di rispondere il prima possibile ogni volta, anche se normalmente richiede un’oretta farlo.
La sola scrittura del commento in risposta sopra, che pure era così dozzinale e incompleto, ha richiesto 40 minuti, più il tempo nei giorni scorsi per ritrovare qualche citazione decente da fare.
a che indirizzo devo scrivere?
A quello indicato nella pagina delle “Informazioni sul Sito”, che poi sarebbe lo stesso riportato in fondo a TUTTE le pagine del sito stesso con la scritta:
Ciao!
nell’articolo tu affermi che nel XIII e XIV secolo l’armatura a piastre metalliche dei cavalieri li metteva al sicuro dalle frecce dei longbow, ma mi viene in mente che a CRECY (1346) gli arceri inglesi fermarono una carica e misero in rotta la cavalleria francese.
Come è spiegabile tutto ciò?
si sente dire spesso che le frecce colpirono per lo piu i cavalli ai fianchi, ma se i cavalli erano in carica frontale come possono essere stati colpiti ai fianchi?
ed inoltre se anche i cavalieri fossero stati disarcionati non potevano cmq affrontare gli arceri a piedi essendo invulnerabili alle loro frecce?
ho scritto qui perche credo che la mia domanda sia attinente al tema della resistenza delle armature dell’epoca.
Di archi lunghi e resistenza delle armature, in particolare anche di Crecy, si è già parlato in questo articolo:
https://www.steamfantasy.it/blog/2008/10/20/performance-arco-da-guerra-inglese/
Cerca il punto dell’articolo in cui c’è questa citazione col blockquote, nella sezione “Il Longbow nell’uso militare e altre informazioni”:
Nella sezione precedente trovi anche l’esempio di Flodden del 1513.
Nel dubbio leggiti tutto l’articolo che qualcosa di interessante lo trovi di sicuro.
Le frecce cadono dall’alto, a parabola, in massa: il tiro teso è molto breve. Nella massa di frecce che ondeggiano nel cielo dall’alto, cosa c’è di strano che cadano sui fianchi (i cavalli non sono bidimensionali), sul sedere, sulla capoccia e sul collo dei cavalli?
Mi stupirei che colpissero il collo dal basso o il ventre a lunga distanza…
Cioè avanzare nel fango, senza alcun vantaggio della carica di cavalleria, facendosi sterminare da uomini d’arme meglio adatti al combattimento a piedi di loro e con armi ad asta specifiche? E in ogni caso senza poter attaccare gli arcieri che erano protetti come sempre da robuste difese di pali appuntiti… in pratica avvicinarsi per scavalcare le difese equivarrebbe a prendersi le frecce da sfondamento a bruciapelo e, in tal caso, la maglia di ferro è altamente probabile che ceda (braccia e gambe non sono protette da cotte di piastre ulteriori, di solito).
Sarebbe stata un’idea furbissima. ^_^
contro una maglia di ferro, secondo i test non erano efficaci i colpi di spada di taglio in quanto nn avevano possibilità di penetrare ma nn si parla degli affondi di punta;
quanta energia poteva sviluppare un’uomo medio in un affondo? era abbastanza per penetrare l’aratura?
C’è il test con la punta di lancia simulata.
Rileggi l’articolo. Se invece consideri stocchi o stiletti o le punte molto acute in cima alle alabarde, usa i dati per le frecce da sfondamento. Per le punte di spada consiglio di stimare una via di mezzo tra la punta piuttosto larga di una lancia e quella molto aguzza di un freccia. Le energie in gioco per un uomo normale sono sempre 60-130, per un energumeno con un’arma manovrata a due mani invece 200 e oltre (dipende da quanto è energumeno e quanto è pesante l’arma, nel limite di massima efficienza tra peso e velocità del colpo).
e per quanto riguarda la lancia in mano ad un cavalire in carica? quanti J puo sviluppare???
Ti rispondo con la stessa precisione che hai dedicato alle domande passate:
tntximi!!!!
Uno: non lo so.
Due: come avrai notato visto che non se ne è mai parlato, non me ne frega nulla.
Tre: quanto basta per sfondare una maglia di ferro (stesso discorso per massa del cavaliere a velocità di carica contro le picche della fanteria).
Quattro: quattro.
Cinque: se sei proprio curioso prova a fare i conti usano la massa della lancia e la velocità del cavallo (credo vada aggiunta anche la massa del braccio del cavaliere… perlomeno il pezzo che collabora sommandosi al peso della lancia).
Vabbé, sono buono: lo faccio io per te.
Immaginiamo un cavallo a 50 Km/h e una lancia di circa 2 kg (non una lancia pesante da cavalleria, immaginiamo una lancia più normale che si possa usare anche a piedi… da ulano, da cavalleggero, da normanno che invade i sassoni nel 1066 o simili): fanno 190-200 J.
Decisamente sufficienti per perforare la cotta di maglia e infliggere una gran bella ferita.
Non ho considerato il peso del dell’arto che contribuisce al colpo con la sua massa (è probabile che quanto meno parte del peso della mano e dell’avambraccio vada sommato se il colpo è esattamente perpendicolare all’asta).
Non ho calcolato il peso del cavallo perché non si trova esattamente dietro la punta, immagino un colpo un po’ laterale in cui il cavallo dà la velocità, ma non la propria massa.
Sono praticamente sicuro che in un calcolo reale, con una macchina che misura gli impatti, alla fine applicando la formula dell’energia cinetica risulti un’energia maggiore e di conseguenza una massa in gioco maggiore di quelle della sola lancia…
Luca, mi sembra che tu abbia un’idea un po’ distorta della guerra. Parliamo di cavalieri, di uomini, non di Iron Man. E gli uomini hanno difficoltà a camminare e combattere nel fango, sotto una pioggia di frecce, con la fanteria nemica che li incalza. Basta cadere in terra e hai chiuso. Chissà quanti di loro sono stati finiti a coltellate e colpi di mazza mentre strisciavano nel fango. Inoltre, è bene ricordare che gli arcieri non erano propriamente i gracili mendicanti compagni di Robin Hood. Erano bestioni di 90-100 chili, incazzati, armati e pronti al corpo a corpo.
ok, un’ultima domanda su una cosa che non ho ben capito dall’articolo: se i cavalieri del 600 indossavano un’armatura a tre quarti di grande spessore 4mm o piu resistenti alle pistole perche portavano cm armi proprio delle pistole che nn sarebbero state efficaci contro i cavalieri nemici? le usavano solamente contro i cavalli? oppure sparavano contro le formazioni di fanteria (se queste avevano armature di minore resistenza)?
Le pistole si utilizzavano in pratica SOLO contro la fanteria, nel caracollo oppure scaricandone una durante la carica per poi rificcarla nella grossa fondina da sella e sguainare la spada.
Contro le armature più leggere dei cavalleggeri possono essere efficaci, a breve distanza, ma fondamentalmente in uno scontro cavalleria contro cavalleria si tirano fuori le spade e ci si massacra. In uno scontro armature pesanti contro armature pesanti, o rischi a beccare con la punta il varco sotto l’ascella quando cercano di sciabolarti oppure puoi colpire lo stivalone di cuoio per spaccargli la gamba (o se arrivi da dietro cercare di infilzare il retro della coscia non protetto).
Non è molto facile né molto efficace… e quindi che fare? Come hai indovinato tu, si ammazza il cavallo! ^___^
Però può anche capitare una combinazione particolare di pistola di grosso calibro a canna molto lunga (o corazziere con carabina e/o moschetto corto) contro altro corazziere con armatura più scadente dell’auspicabile (le dichiarazioni false nelle “prove” delle armature nel ‘600 erano la NORMA, lo si è scoperto studiando i marchi di prova lasciati dai proiettili su corazze di qualità e spessore noto… si usavano armi da fuoco con cariche notevolmente alleggerite ^_^ come spiega Alan Williams nell’articolo apparso su Gladius): in tal caso un bel proiettile a bruciapelo può fare un gran bell’effetto!
^_^
scusa , ma a quanto leggo, nel XV secolo, un soldato in un’armatura milanese era praticamente invulnerabile a qualsiasi tipo di arma da lancio disponibile al tempo, quindi gli scontri in quel periodo, a rigor di logica, dovevano svilupparsi per lo piu in corpo a corpo???
ma allora gli arceri che avevano avuto un ruolo cosi di rilievo nel secolo precedente avevano perso il loro valore in campo???
Tendenzialmente il corpo a corpo è rimasto risolutivo fino all’introduzione del fuoco rapido su più file a fine Cinquecento.
Nel caso di un soldato con l’armatura migliore possibile per il ‘400, un’ottima armatura milanese, possiamo considerare la corazza a prova di freccia, balestra e cannone manesco hussita. La corazza, appunto, dove lo spessore è circa 2 mm. Gli arti sono di norma meno spessi perché contengono bersagli meno importanti da proteggere e il cavaliere / uomo d’arme vuole ridurre al minimo il peso dell’armatura “utile” per non subire affatticamento nelle lunghe battaglie (una cosa è fare un duello o una giostra avvolti nell’armatura più invulnerabile immaginabile, un’altra cosa è resistere ai colpi di sole, alla fatica, alla sete e a un eventuale svenimento per lo sforzo prolungato con un’armatura pesantissima in un intero pomeriggio di battaglia).
Braccia e gambe (o la schiena dell’armatura), seppur sempre molto ben protette da larghe punte di lancia, lame e frecce, potrebbero cedere (poco o in modo disastroso) contro proiettili di cannoni maneschi o contro dardi di balestra pesante. O anche contro le punte acuminate dei martelli d’arme o piegarsi sotto gli impatti consecutivi di una mazza o di una morning star, mentre ci si trova a terra a strisciare, impossibilitati a rialzarsi dai colpi.
Ti propongo due esempi di spessori.
Armatura tedesca, di Augusta, circa 1510, collezione Wallace.
Petto: 1,3 mm
Schiena: 1 mm
Cranio dell’elmo: 1,5 mm
Gambe (sotto il ginocchio): 0,8 mm
Spalle: 1,1 mm
Fiancali: 0,8 mm
Cosce: 0,7 mm
Gorgiera: 1,1 mm
Tutto in acciaio di altissima qualità, pari a un fattore W di 1,5 o 2. Disponendo di un armaiolo in grado di fabbricare acciai tanto buoni, l’acquirente deve aver optato per la massima leggerezza: robusta come un’armatura milanese (o quasi), a peso molto minore. E’ chiaramente un’armatura pensata per il corpo a corpo.
Armatura austriaca, di Innsbruck, 1563, museo nazionale estone.
Petto: 1,9 mm
Schiena: 1,2 mm
Cranio dell’elmetto: 1,4 mm
Fiancali: 0,9 mm
Stesso acciaio di altissima qualità, mezzo secolo dopo: lo spessore dell’armatura perlomeno a 1,9 mm è ormai obbligatorio per resistere ai colpi di moschetto a 100 metri e ai colpi di pistola a bruciapelo. Come sempre si è alleggerito dove possibile: fiancali e schiena.
L’armatura non protegge in ogni caso in alcune aree: inguine, sedere, retro della coscia e ascelle sono di solito coperte dalla sola imbottitura (con al massimo un po’ di cotta di maglia, sotto forma di pezze localizzate cucite sull’imbottitura o di un gonnellino apposito indossato con un cinturino). La penna aguzza di un martello d’arme, con la sua angolatura a 90 gradi rispetto al manico, è ottimizzata per entrare nei varchi delle ascelle quando si apre lo spazio in seguito a un fendente. Non è facile, non è nulla facile contro un nemico coperto di armatura, ma si può tentare.
Se il cavaliere è stato atterrato, sgambettandolo con un’arma ad asta o spingendolo al suolo con la violenza dei colpi, si può sempre provare a saltargli addosso, alzargli a forza la visiera e tempestarli la faccia di colpi di pugnale fino a distruggere naso, bocca, occhi… quello che capita.
Se hai letto l’articolo sull’arco lungo che ti avevo indicato, hai già visto come l’arco lungo non fosse più al passo coi tempi all’inizio del ‘500.
ok, ho capito, ma le spade venivano usate ancora in questo periodo, ovvero a fine 300 – inizi 400? che danni si poteva causare con una spada su un cavaliere o un fante corazzato con le armature di buona qualità di cui ai parlato?
Come già spiegato in questo articolo, con la spade non fai NIENTE contro le armature di quel tipo.
Però puoi provare a colpire dove non sono presenti: il volto (se possibile), il retro della coscia e il varco delle ascelle (magari lottando con l’arma in presa stretta, una mano sull’elsa e una sulla lama come mostrato nel Flos Duellatorum).
Già. Conta che io con una zweihander da 3.7 kg sono riuscito a rompere un solo anello di una lorica hamata. Ho colpito due volte con tutta la forza, con un fendente e un dritto sgualembrato, nello stesso punto. Certo, di sicuro avrei rotto la clavicola del malcapitato, ma ho idea che già una maglia ad anelli possa essere un ostacolo insuperabile per provocare ferite con il taglio di una lama. Il discorso cambia se parliamo di colpi con la punta.
e in che termini cambia con i colpi di punta Zweilawyer?
ma se si colpisse un soldato corazzato con una spada o con una alabarda alla testa, che danni si potrebbe procurare??? era questa il bersaglio che cercavano per i colpi di taglio???
– Colpendo con la punta si può bucare una maglia ad anelli, ma non è facile come si vede nei film. Ci vogliono forza, velocità, e una spada adatta. In questo senso il gladio era un’ottima arma.
-Anche con elmo ed imbottitura, un colpo forte alla testa poteva essere letale. Ma tieni conto che le rotondità degli elmi, specie quelli dal XV secolo in poi, erano studiate per far scivolare i colpi sulla superficie metallica, disperdendone la forza. Se avessi solo una spada (e su quale tipo di spada potrebbe aprirsi un nuovo discorso..stop! Non chiedere, prima studiati le tipologie di Oakeshott:)), cercherei di colpire un uomo d’arme alle giunture dell’armatura, agli occhi (con tecniche di mezza spada, alle braccia, e alla parte inferiore delle gambe.
potresti cmq solo rompere le ossa, nn ferire di taglio, è corretto?
innanzitutti complimenti per il tuo articolo, è veramente ben fatto.
leggendo gli ultimi commenti pero mi è sorto un dubbio: è stato detto che il miglior modo per neutralizzare un uomo d’arme, ipotiziamo del ‘400 – ‘500, era colpire nei punti di giunzione dell’armatura o algi occhi, ma mi viene in mente che le parti suddette erano comunque protette da cotte di maglia o altro; era dunque possibile forare questultima, o i colpi erano portati unicamente al volto per cercare la feritoia della celata?
Non erano sempre-sempre protette. Non è automatico che con ogni armatura bianca vi sia assieme una veste imbottita con pezze ascellari in maglia metallica: più facile che vi sia solo il gonnellino in maglia o nemmeno quello.
Spesso c’era solo la veste antiurto formata da strati di tessuto cuciti assieme e altre volte l’armatura era indossata direttamente sopra vestiti spessi, ma “non così tanto imbottiti” (come si vede in molte raffigurazioni di doppisoldo lanzichenecchi in mezza armatura).
Nel caso di pezze di maglia di ferro, immagino che l’unica spada in grado di penetrarle fosse l’Estoc, con la sua punta da sfondamento aguzza.
Nel caso della veste imbottita senza pezze, magari bastava un colpo violento con una spada a una mano e mezza tenuta in presa stretta, con una mano sulla guardia e una sulla lama per guidare il colpo di precisione.
Rimane comunque molto difficile colpire un nemico lì sotto: meglio sparargli. ^_^
Più facile mirare al volto, bersaglio prediletto anche degli arcieri inglesi nei pochi casi in cui potevano mirare a un singolo nemico (ovvero quando il nemico era a pochi metri, a sgambettare contro i cavalli di frisia posti davanti agli arcieri). Spesso il volto era scoperto, dato che lottare a lungo con la faccia foderata di metallo doveva rendere il tutto ancora più faticoso… già viene il fiato corto a lottare, figuriamoci con la respirazione ridotta dai pochi buchi nel metallo: mezzi sordi per l’elmo, mezzi orbi per la visiera stretta e pure ansimanti per la faccia coperta… non proprio una cosa che si possa fare molto a lungo.
Se invece è tutto coperto, dalle ascelle al retro delle cosce, con appena una fessura per gli occhi, come nella famosa armatura per lizza da fante di Enrico VIII… non resta che sparargli! ^__^
Esistono le armi da fuoco per un buon motivo e la carne “troppo in scatola” ne merita sempre una dose per ricordargli chi comanda.
Orsù, rimangiati queste parole ignominiose!
Bang!
Ho fortunatissimamente trovato questo sito che trovo eccezzionale. Vorrei fare i più grandi complimenti al SIG. DUCA che trovo STUPEFACENTE per la SUA ENORME CULTURA.Quindi mi permettererò poi di FARLE alcune domande.INFINITI CDMPLIMENTI. Distinti Saluti.
Salve
Innanzitutto volevo fare i complimenti per questo articolo superbo, era da tempo che cercavo questo tipo di informazioni. Poi vorrei fare una domanda: un armatura di acciaio qualità III diciamo, quanto dovrebbe essere spessa pe poter resistere a un proiettile di 4000 J?
(in parole povere vorrei sapere come dovrebbe essere spessa un armatura di acciaio (III o anche IV) per poter resistere alle pistole moderne)
Distinti saluti e complimenti ancora per l’articolo.
Ciao.
Usando la formula di Krupp, un proiettile tondo in piombo morbido da 18 mm sparato da un moschetto da posta e avente all’impatto 4000 J come richiesto…
…può penetrare un massimo di 3,54 mm di acciaio 1,1 più resistente del mild steel. Se fosse una palla in piombo duro, come erano di solito le palle nel Settecento (legate con un 5% di antimonio o quel che era, ho degli articoli da parte sulla durezza del piombo), la penetrazione salirebbe a ben 4,42 mm… o forse a 4 mm, se non è poi così eccellente il livello di durezza (non mi ricordo se ci si rimangia tutto il 20% di perdita o solo la metà, dovrei frugare negli appunti che avevo quando ho studiato queste cose un sacco di mesi fa).
Ricordo che la tabella in cima, nell’articolo, usa sfere da 20 mm in acciaio per la simulazione, mentre il piombo morbido penetra solo l’80% di quanto farebbe un pari calibro in metallo indeformabile ai fini del test (la palla d’acciaio, appunto).
Passando alle pistole moderne.
Prendiamo una in 9×19 con palla FMJ (piombo con blindatura) da 8 grammi, 350 m/s alla bocca, 490 J.
Può penetrare secondo la formula 2,33 mm di acciaio dolce.
Se immaginiamo acciaio leggermente migliore (classe III), scende a 2,16 mm.
Se immaginiamo un’armatura in classe IV, 1,5 volte più resistente dell’acciaio AISI 1010-1020, la penetrazione scende a 1,72 mm circa.
Credo che i conti siano giusti.
mi hai dato piu informazioni di quanto fossero necessarie.
Grazie Duca e complimenti ancora per il blog.
Salve sono di nuovo io, trovo molto interessante l’armatura di Enrico VIII però mi chiedo se era protetta anche sotto le ascelle e fra i genitali e il sedere (da sotto), se si mi chiedo come fosse possibile proteggere anche lì.
Inoltre ho letto nel blog che alcune armature sono arrivate a sfiorare gli 8mm di spessore e mi chiedo se era davvero necessario un tale spessore per resistere a cosa?4
grazie per la pazienza queste cose mi hanno sempre affascinato.
C’è una armatura di Enrico VIII che è protetta proprio ovunque.
È un’armatura molto particolare, sviluppata in occasione delle lizze per fanti del 1520 al tempo dell’incontro con Francesco I, che con un ingegnoso sistema di lamelle copre ogni possibile punto debole solitamente lasciato scoperto (retro delle cosce) o al più coperto da maglia di ferro (ascelle, sedere, genitali).
Puoi immaginare che un’armatura simile non solo è appesantita andando a coprire aree considerate “sacrificabili” in un’armatura da guerra (si cerca sempre un compromesso tra pesantezza e protezione), ma deve essere anche molto scomoda a meno di non stare sempre e solo in piedi! La lamelle metalliche, per quanto buone, non penso fossero il top della comodità quando ci si sedeva e… beh, il culo interamente di metallo credo si commenti da solo. Per non parlare di quel poco di areazione data dai punti scoperti che qui va a farsi benedire. ^_^
C’è una bellissima doppia foto di quell’armatura speciale, davanti e dietro, in The Armourer and His Craft di Charles Ffoulkes (p.28 edizione Dover del 1988).
In realtà non è mai stata usata: è rimasta incompleta nelle rifiniture (è stata lucidata, facendola sembrare finita, solo in tempi recenti) perché all’ultimo cambiarono le regole del torneo ed Enrico VIII dovette procurarsi un’altra armatura che rispettasse le nuove regole. ^_^
La foto dietro e davanti:

Cliccare per ingrandire
The Knight and the Blast Furnace invece ci svela con una foto al microscopio il tipo di acciaio usato: un miscuglio di perlite e ferrite. Non proprio il top della qualità, ma d’altronde le produzioni inglesi all’epoca non potevano ancora competere con quelle italiane (quelle francesi erano pure peggiori).
Come hai visto, nel caso di palle di grandi dimensioni contro lamine di dimensioni ridotte (spessore corazza inferiore a 1/5 del diametro del proiettile tondeggiante) entra in gioco una sorta di sconto nell’energia necessaria all’asportazione per “spinta” del metallo investito dalla palla (la palla taglia un tondino di metallo inferiore al proprio diametro e spinge in fuori il resto, per passare), tanto che nel caso di pistole .45 contro elmetti spessi 1,1 mm (caso che ho potuto simulare correttamente proprio grazie a questa consapevolezza del bizzarro comportamento delle “lamine sottili”), come avveniva nei test della Grande Guerra, l’energia necessaria alla perforazione arriva a essere la metà rispetto a quella ipotizzabile con la formula di Krupp (un rapporto 1 a 10 porta a un dimezzamento dell’energia in Joule richiesta, circa).
Affrontando grandi moschetti da posta (19-25 mm), come quelli del ‘500 e ‘600 in mano ai fanti più robusti o ad alcune truppe a difesa delle fortificazioni, è necessario contrapporre GRANDI spessori di armatura per far sparire lo “sconto”. Naturalmente all’epoca non sapevano nulla delle lamine sottili o simili, ma avevano una conoscenza empirica di cosa fermasse cosa (e, ok, nelle produzioni di massa spesso truffavano i clienti, come l’analisi delle armature da corazziere portoghesi fatta da Alan Williams ci insegna).
D’altronde vedi anche tu, nella tabella riferita a proiettili indeformabili da 20 mm, che enorme differenza in resistenza vi sia tra 2 mm e 4 mm di acciaio AISI 1015 (raddoppia lo spessore, raddoppia il peso… ma più che quadruplica la resistenza! Da 750 a 3400 J!).
Poi ci sono delle considerazioni di ordine pratico e tecnico sulla produzione delle armature. All’epoca era molto difficile controllare la qualità dell’acciaio, in particolare se il “blumo” cresceva di dimensioni. Fino a blumi di piccolo peso (non ricordo benissimo i limiti, ma sono scritti nel libro di Williams), ad esempio quelli necessari per fare un petto di armatura di 2 mm o la lama di uno spadone ecc… non c’erano problemi, ma appena il blumo diventava ingombrante (come quello per fare un petto di 4+ mm), il blumo non riusciva a smaltire le scorie nella lavorazione e il carbonio si mischiava poco e male… veniva, insomma, il ferraccio da armatura da corazziere dell’esempio in fondo all’articolo!
A quel punto, per fermare un moschetto da posta da 19-25 mm con un simile ferraccio (e non solo una pistola a bruciapelo o un moschetto a qualche decina di metri), bisogna aumentare ancora lo spessore: 6-8 mm!
Costa meno fare un’armatura più robusta perché di acciaio peggiore e più spesso, che non farne una di eccellente acciaio di prima qualità più sottile. Costa meno ed è molto più facile trovare centinaia di armaioli in grado di farla senza sforzo (trovarne in grado di fare armature della più alta qualità è molto difficile, anche disponendo dei soldi). Il prezzo da pagare è il maggior peso.
Un trucco per fare armature molto robuste preservando però la qualità degli acciai e senza salire troppo di spessore, era quello di imbullonare/inchiodare due corazze distinte tra loro: entrambe spesse 2 mm, entrambe di buon acciaio, permettono uno spessore finale di 4 mm tutto in buon acciaio (qualità III o poco meno) e non in ferraccio!
Svantaggio: i costi della lavorazione raddoppiano perché sono, a tutti gli effetti, due corazze distinte.
Questo trucco delle Duplex Armour si poteva usare anche per riciclare corazze di bassa qualità, ma con caratteristiche diverse. Così una corazza di martensite mal rivenuta, dura e fragile, si può inchiodare su una in ferro battuto più morbido, ma anche più capace di piegarsi senza spezzarsi offrendo un sostegno alla fragile corazza sovrastante… la combinazione di durezza e resistenza morbida permette di creare un’armatura “ibrida” con doti intermedie tra le due corazze, salvando il salvabile. ^_^
Venne poi riscoperto è applicato nell’Ottocento dal geniale Krupp per le armature navali: acciaio fragile e durissimo (grazie ai bagni di carbone caldo per saturarlo di carbonio) all’esterno, per spezzare/deformare i proiettili nemici, e dentro acciaio dolce o ferro battuto molto meno duri, ma molto più resistenti al crack.
Superbo.
I miei complimenti per un articolo completo sotto ogni punto di vista. Mi servirà ampiamente per la mia attività di combattente e rievocatore.
Solo una cosa, Duca: perché non pubblichi…?
MOLTO INTERESSANTE, DIVERSO E COMPLETO!!!
Grazie Luca
Avrei voluto studiare questo pomeriggio, invece mi sono trovato a divorare i tuoi post uno dopo l’altro. Mi tolgo il cappello
Ottimo, sono felice di aver collaborato a tenere gli studenti lontani dall’inutile studio. ^_^
Rimettiti il coperchio che fa freddo.
Vostra Grazia, rileggendo questo articolo mi è sorto un dubbio: a cosa è dovuta la differenza di joule fra un proiettile di cannone manesco e uno di moschetto a miccia? È una questione di lunghezza della canna, calibro o cosa?
L’energia cinetica è data da massa per quadrato della velocità.
La velocità è data, in parole povere, dall’energia che la polvere può cedere e da quanta ne cede per accelerare il proiettile. La cede tutta se brucia tutta e brucia tutta se canna sufficientemente lunga.
Nel caso delle armi da fuoco prima del ‘500, i problemi erano la polvere non in grani porosi (la carica nel ‘300-‘400 è una massa di polvere sabbiosa che lascia poco spazio all’ossigeno e quindi c’è meno spinta perché brucia più lentamente lungo la canna) e il fatto che le armi hussite non avessero canne molto lunghe per farla bruciar tutta. In pratica una bella nuvola di polvere bruciava per aria, senza spingere il proiettile.
Riporto da vecchio articolo:
^_^
Ecco, proprio su questo punto mi sorge un altro dubbio: in che epoca, esattamente, si è cominciato a “granificare” (spero che questo verbo esista!) la polvere? Wikipedia parla di “tardo 14° secolo”, ossia fine ‘300, ma da quanto scrivi deduco che sia completamente sbagliato.
Alan Williams indica i primi decenni del ‘500 come periodo in cui la polvere in grani è diffusa come standard.
Bert Hall in Weapons and Warfare in Renaissance Europe dedica un intero capitolo alla storia della polvere da sparo e alla lavorazione in grani, riportando grafici di pressione e dimensioni dei grani tipiche del XIX secolo (le misure da Fg a 4Fg che, grossomodo, usano tutti per intendersi).
Il primo a parlare in modo preciso del metodo “avanzato” di lavorazione della polvere in grani (quindi non la semplice frattura in grossi e grossolani knollen fatta dai crucchi già a inizio ‘400) è Whitehorne nel 1562.
Whitehorne in realtà plagia il capitolo sulla polvere da sparo di Biringuccio in Pirotechnia, ma aggiunge alcune righe dedicate nello specifico al fatto che la polvere sia in grani.
Anche Biringuccio e Tartaglia conoscevano il metodo di lavorazione in grani e lo citano, seppure non nel dettaglio e in modo specifico come il successivo Whitehorne.
Secondo Hall gli anni 1530 sono quelli in cui la polvere in grani, fini e suddivisi in modo preciso per dimensione, si affermano come standard militare.
Prima l’uso poteva esserci, ma non standardizzato. Wikipedia con la fine del ‘300 probabilmente confonde i knollen con la lavorazione in grani.
È facile quindi che i cannoni usassero ancora polvere in grossolani knollen (giusto per non doverla rimestare sempre quando le componenti si dividono) fino ai primi decenni del ‘500, ma gli archibugeri specializzati come i lanzichenecchi usassero già fin dagli esordi polvere in grani.
Ottimo, grazie mille ^_^
Potrei fare un articolo di base sulla polvere da sparo, niente di particolarmente complesso, sul modello di quelli presenti nei primi capitoli dei libri sul tiro ad avancarica (con aggiunte di informazioni storiche prese da Hall).
Sembra un argomento che può interessare.
CIAO DUCA
SCUSA IL DISTURBO
SE NON MI SONO RINCOGLIONITO ANNI FA AVEVO LETTO CHE I CAVALIERI FRANCESI DEL 500 (AI TEMPI DI FRANCESCO I) SOPRA LA CORAZZA PORTAVANO UNA SPECIE DI GIUBBOTTONE (CHIEDO SCUSA DEL TERMIEN) FATTO TIPO UN INSIEME DI “SALAMI” RIEMPITI DI STOFFOA O QUANT’ALTRO PER FARE PROTEZIONE ULTERIORE CONTRO LE ARMI DA FUOCO DELL’EPOCA.
NEI DIPINTI DELL’EPOCA MI SEMBRA DI AVER VISTO QUALCOSA DI SIMILE.
SARA’ VERO?
CIAO …SEI GRANDE.
RAFFAELE
Ciao!
Non ne ho idea. Di spessissimi gambeson se ne usavano parecchi nel ‘300, prima dell’arrivo delle armature a piastre, ma non ricordo questo uso specifico antiproiettile successivo. Anche perché a meno di non usare strati su strati di seta a filo lungo come certe giubbe antiproiettile asiatiche dell’800 (seta indiana quindi, non americana a fibra corta), l’ingombro sarebbe tale da rendere più sensato un rinforzo della corazza in metallo (travestiti da omini Michelin non so quanto combatterebbero bene) magari con una piastra aggiuntiva inchiodata come nelle corazze duplex del ‘500-‘600.
Ricordo però che sopra e/o sotto le armature mettevano dei bei vestitoni e/o soprabiti caldi, come quelli che si vedono nei dipinti sulla battaglia di Pavia del 1525. L’acciaio delle armature effettivamente non protegge dal freddo…
Bellissimo sito Duca. Vorrei sottoporle due domande ,un po ingenue, parzialmente correlate all’articolo:
1 Dal suo interessante articolo si evince la quasi totale inutilità di qualunque spada contro anche un minimo di armatura, ciononostante la spada è stata considerata, anche da i contemporanei dei cavalieri come l’arma per eccellenza della cavalleria, la domanda è questa: perché proprio la spada e non la mazza o la lancia, molto più efficaci secondo il test?
2 Girovagando per internet ho notato questo articolo che parla di doppie maglie, crede che questo tipo di protezione sia realmente esistita? se si come pensa che la cosa abbia influito sulla protezione da frecce e quadrelli?
grazie in anticipo e a risentirci.
1- La spada è più versatile ed è più indossabile in contesti civili. Comunque anche mazza e lance non possono niente contro le armature minimamente spesse (a meno che la lancia non sia usata con una carica a cavallo -gli Ulani usavano lance e costrinsero Napoleone a dare le corazze anche ai carabinieri a cavallo perché in scontri spada contro lancia venivano massacrati-). La mazza è buona, finché lo spostamento di massa e del punto di percussione più distante possibile dalla mano permette ancora di spaccare le ossa sotto una cotta di maglia (invece di causare un ematoma) o di piegare un bracciale/gambale da 0,7-1,2 mm, che era lo spessore più comune (anche quando la corazza era da 2-2,5 mm). Meglio ancora il martello da guerra, con il becco tipo punta bodkin per sfondare le piastre meno spesse o di acciaio di qualità inferiore: dove la mazza non riesce, può il martello da guerra.
http://upload.wikimedia.org/wikipedia/commons/6/6b/Moritz-von-Sachsen-1578.jpg
Se i nemici hanno solo corazza (2-3 mm) e il resto è difeso solo dall’uniforme, la goffa mazza (poco pronta a difendere dopo un attacco -o a difendere in generale-) non va bene. Meglio allora una sciabola, pesante (la M1860 pesante USA era da 1,2 kg o poco più) o anche solo leggera (M1796 leggera inglese da 1 kg o poco meno), accompagnata alle pistole o alla carabina, come avvenne dal ‘500 fino all’inizio del ‘900.
Strappare le uniformi in panno di lana del ‘700-‘800 non è comunque facile nemmeno per una spada. Patton nel suo manuale sulla nuova spada statunitense del 1913 cita i francesi del tempo di Napoleone, invidiosi delle sciabole super-taglianti inglesi (stile “tagliente come una katana da anime giappo”) che potevano fendere le divise, ma poi gli inglesi a loro volta erano invidiosi delle pesanti spade dritte dei corazzieri francesi, capaci di perforare le uniformi. In realtà tutti e due avevano i loro bei problemi a penetrare gli spessi tessuti delle divise (e i francesi di punta, pur con la penetrazione assicurata, dovevano mirare allora alla cassa toracica per rendere incapace di risposta il nemico all’istante… non sempre facile scegliere quel bersaglio escludendo braccia o stomaco).
Non per niente il bersaglio principale di chi doveva di preferenza fendere, gli inglesi, era il volto scoperto (i kepì e pickelhaube in cuoio spesso del periodo sono a prova di spada). In alternativa le braccia: con un po’ di fortuna si poteva spaccare le ossa, anche quando la lana pesante (più fodera più maglia dell’intimo sottostante e con sopra il cappotto delle divise invernali) tratteneva il taglio.
2. È un vecchio articolo per Gurps, mi pare di 6 anni fa.
Le maglie con anelli più grossi oppure con più anelli inseriti esistevano. L’alternativa di Flori di intendere la maglia doppia come due maglie una sopra l’altra mi pare cretina (o comunque, come dice Flori, di emergenza e sparita in breve tempo): più facile fossero anelli pesanti il doppio (doppio del metallo da sfondare, doppia -o più- resistenza) o il doppio degli anelli con uno schema 8-2 invece di 4-1:
http://upload.wikimedia.org/wikipedia/en/1/10/Kings_mail.jpg
Il doppio del metallo da sfondare, molto meno spazio vuoto per mantenere la mobilità e la capacità di essere indossata anche se si aumenta di taglia. Tanto vale fare le piastre, allora…
Grazie mille per la risposta più che esauriente :)
Ma sei un mago! Non hai idea di quanto mi saranno utili queste informazioni! Grazie davvero!
Duca, volevo sapere se è possibile che una lancia da tiro con una punta adatta e acciaio di qualità possa trapassare una cotta di maglia.
La lancia sarebbe lanciata da un bestione, un tipo alto quasi due metri con braccia che sembrano tronchi d’albero, ma il fatto è che più spesso hai scritto che è difficile calcolare la resistenza delle cotte di maglia a causa della ridotta dimensione degli anelli (oppure sono io che ho capito male), dunque non saprei rispondere a questa domanda che, purtroppo, mi sarebbe piuttosto utile sapere per un racconto che ho in mente.
Chris.
Mancano informazioni, ma ti do uno spunto. Immaginiamo che le punte siano più dure dell’acciaio che colpiscono, come hai richiesto e come è avvenuto nel test citato da Williams.
Immaginiamo una lancia con una punta tipo freccia, aerodinamica e da sfondamento, non larga / a foglia ecc…
La possiamo approssimare alla punta da freccia che ha richiesto 120 J per sfondare cotta di maglia di qualità “minima/normale” (le cotte di maglia peggio non credo possano essere perché Williams spiega che le inclusioni di scorie in fili sottili NON sono possibili… ha anche riportato uno studio sui campioni disponibili e la qualità non arriva mai a quella del “ferraccio da munizione”).
I problemi diventano: peso del giavellotto e velocità all’impatto.
Oppure: peso del giavellotto, velocità al lancio e quanta velocità perde durante il volo.
È lo stesso. Proviamo col secondo.
Immagino un giavellotto come se fosse una lancia di peso inferiore a quello di una lancia da corpo a corpo. Casualmente immagino pesi, uhm, 800 grammi. Ok, ho scelto 8 etti perché è il peso del giavellotto olimpico maschile e ho già dei dati da usare. ^__^””
Che velocità ha un giavellotto olimpico maschile e che gittata ha?
Boh! Usiamo i dati suggeriti qui:
http://www.worldofjavelin.com/posts/biomechanics-release-velocity/
Dai 24 m/s ai 30 m/s (63,8-93,8 metri di gittata con un lancio ad angolo di 40 gradi).
A 25 m/s un oggetto di 800 grammi ha 250 J. Wow. Se immaginiamo che un oggetto pesante come il giavellotto abbia perso solo un terzo dell’energia iniziale al momento dell’impatto, sono ben 160 J! Troppi, temo.
Peccato che quelli siano dati di lanciatori olimpici. E le gittate sono mostruose per delle lance usate davvero (oltre al problema di colpire qualcuno a 60+ metri così, ma se uno è bravo… peccato che il nemico se appena appena vede il tiro ha 3-4 secondi per schivare, grossomodo il tempo di volo, per cui col cavolo che lo prendi).
A che velocità lancerà un essere umano più normale?
Forse tra i 15 e i 20 m/s? Cioè 90-160 J al lancio e 60-100 J all’impatto con la perdita ipotizzata prima.
Non basta per passare l’armatura, a meno di non lanciare a distanza molto ravvicinata.
E se il giavellotto pesa di più, se è un modello con un peso sui 1,3-1,5 kg come un pilum romano leggero?
http://zweilawyer.com/2010/03/14/le-armi-del-legionario-il-pilum/
La nuova energia cinetica va ricalcolata partendo dalla quantità di moto per stimare la nuova velocità col nuovo peso. Coi proiettili funziona: data una carica di lancio nota, la perdita di velocità è proporzionale all’aumento di peso del proiettile, con conseguente crollo dell’energia cinetica.
Immaginiamo il lancio a 20 m/s. 20×0,8 = 16
16 / 1,4 = 11,4 m/s
Facciamo 12 m/s? Signora, lascio?
A 12 m/s al lancio per 1,4 kg di peso fa poco più di 100 J al lancio (grossomodo come un’arma da corpo a corpo, 60-130 J per un uomo normale) e circa, solita ipotesi farlocca di ritenzione dell’energia come se fosse una freccia pesante, 60-70 J all’impatto.
Non passa la maglia. Ok, ce lo aspettavamo, infatti è meglio usare gli archi da guerra pesanti…
Magari un bestione che lancia un giavellottone abbastanza pesante da sfruttare tutta la sua forza ottiene di più: 150-200 J. Allora non c’è problema, fora.
Proprio 200 J era stata l’ipotesi di Williams per un tizio muscoloso armato di alabarda / ascia danese.
Impatto dove? Boh!
Sì, non me lo hai chiesto, ma tanto sto a cacare cifre a caso e tanto vale proseguire.
Non ho voglia di calcolare le gittate, approssimare col punto, controllare con i dati della tabella del giavellotto per ricondurre la formula generale al caso reale ecc… due coglioni.
Grossomodo la tabella, a occhio, ci mostra che la gittata aumenta un po’ meno dell’aumento dell’energia cinetica. A 30 m/s ha 1,56 volte l’energia del giavellotto a 24 m/s e vola 1,47 volte più distante. Un 5% in meno rispetto alla progressione algebricazzi.
Tra 24 a 25 m/s le cose vanno meglio: la differenza è di un 1% circa a svantaggio della gittata.
Farlocchiamo una ipotesi di gittata passando da 24 a 20 m/s, poi tanto abbiamo ricalcolato con la nuova massa portando a 12 m/s, ma la quantità di moto è quella.
Pim pum pam… 45 metri di gittata? Facendo al dimezzamento da 24 a 12, con lo scarto del 10% in più per la differenza, fa 35 metri.
Zwei dice che i pila leggeri a 35 metri li lanciavano. Un’altra fonte dice che la gittata massima non supera i 50 metri. Direi che una stima di 35-45 sia accettabile per un pilum di 1,4 kg.
Duca, sei un punto di riferimento importantissimo per me. Risposte così ad una domanda in un commento non si trovano da tutte le parti. Anzi, praticamente da nessuna parte.
Grazie davvero, non ho parole.
Rifletterò bene allora prima di dire “La lancia colpì il cavaliere e lo gettò a terra. Il petto trafitto vomitava sangue” :D
Un’altra cosa, se io sono il generale dell’esercito e possiedo come numero di forze solo fanteria pesante (di stile vichingo, armati di Asce a Due Mani, Spade Lunghe, Scudi e, appunto, le Lance piuttosto robuste su cui mi domandavo prima), cosa posso fare contro una carica di cavalleria pesante? Mi riferisco alla cavalleria del 12 secolo, stile primi crociati, con maglie di ferro e non corazzati come quelle degli ultimi secoli.
Io non posseggo arcieri e quindi non posso rispondere tentando di far fuori i cavalli, ma ho a disposizione le lance. Avrebbe senso tentare, appena raggiungono una distanza accettabile, di lanciare con la prima fila dei miei uomini le lance contro i cavalieri? Oppure sarebbe del tutto inutile?
Nel racconto gli uomini che ho a disposizione sono dei bestioni, alti minimo un metro e ottanta e massimo due metri (come dicevo prima, appunto).
Non ti chiedo di fare altri calcoli, non voglio abusare della tua pazienza (immagino quanta fatica ti sia costato rispondere alla prima domanda), ma mi chiedevo se varrebbe la pena tirare per tirar giù qualche cavaliere o, più sensato, i destrieri stessi (cosa che creerebbe un po’ di confusione nelle file della squadra di cavalieri).
Il mio è solo un tentativo di rendere un po’ meno arduo il confronto tra i due eserciti che si affrontano, perché la mancanza di tiro e di cavalleria dei simil-vichinghi li rende alquanto indifesi contro la cavalleria e il tiro degli archi lunghi avversari.
Insomma, varrebbe la pena tentare di colpire i cavalieri in carica oppure no?
P.s: La carica dei cavalieri, inoltre, non renderebbe l’impatto con le lance ancor più violento e facilitando la penetrazione delle lance?
Io non so se sia possibile colpire un cavaliere in corsa, ma tirando con un rango di diverse decine di uomini contro una squadra di 20 cavalieri per fila in un’unità di tre (così ho letto facevano una volta, spero di non aver trovato scritta una cavolata) mi pare difficile non riuscire a colpire qualcuno e creare confusione in quelli dietro di loro. Una volta che l’unità perde la furia della carica e i cavalieri inciampano l’uno sull’altro non penso sia difficile andare a finirli con asce e spade.
Ovviamente ciò è tutta teoria e magari dico solo cazzate, ma meglio chiedere riguardo a delle cazzate prima di scriverne (meglio non fare figure stile Donne e bambini che imbracciano archi e tirano piogge mortali…)
È meglio che riescano a tenere una formazione compatta. Quindi ok una scarica di lance da tiro (con punte strette a aguzze) contro la cavalleria, e poi subito tutti con la lancia da combattimento (immaginiamo lunga 2-3 metri, con la punta larga) ben puntata in avanti per impedire ai cavalieri di avvicinarsi o sfondare in carica la formazione.
Sì, come immaginato la velocità relativa conta.
Se i tuoi superbestioni tirano giavellotti pesanti (2 kg), come i pila pesanti romani, a 15 m/s… fanno a bruciapelo 225 J. D’altronde sono superbestioni, tirano a gran velocità anche armi molto pesanti (un po’ come il concetto dell’arco: più sei forte e più usi archi forti atti a lanciare, alla stessa velocità, frecce più pesanti).
Ma se investono nemici in carica a… mettiamo 10 m/s?
Si somma, 25 m/s. Possiamo proprio sommare perché non ci sono altri accorgimenti da conteggiare,la parabola non è curva come nelle frecce a grande distanza -dove comunque i cavalli vanno piano-, qui immaginiamo un tiro piuttosto teso contro una carica in atto.
Con 25 m/s, immagina una eventuale scarica a bruciapelo a pochi metri (ma poi finiscono loro addosso i cavalli e i cavalieri feriti per cui la “carica” ha successo parziale lo stesso), sono ben 625 J. In pratica dei colpi di pistola.
Mettiamo che sono più distanti e i giavellotti stanno già rallentando un po’… 10+10 fa 20 m/s, viene 400 J.
Siamo ancora nell’ambito pistole e grandi balestre da posta che tirano dardi enormi. ^_^””
Aspettiamo il parere di Zwei.
Fantastico!
Il mio problema è che i miei “superbestioni” non posseggono lance lunghe 3 metri (li ho voluti mantenere più sull’aspetto vichingo e a quanto mi risulta questi ultimi non se ne sono mai serviti, anche se, c’è da dirlo, non ne hanno mai avuto bisogno, visto che compivano per lo più dei raid… mi sa che dovrò riflettere un po’ su questo aspetto).
Ma con una potenza tanto mostruosa posso persino passare da parte a parte un cavaliere? O.O (Perché l’immagine è… wow! Se è possibile la voglio scrivere, diamine!)
Te li ho calcolati come bestioni veri e propri. Tirano bordate di lance, pesanti, con il doppio dell’energia cinetica di un normale legionario ipotizzato all’inizio.
Sfondano cotta di maglia, imbottitura e affondano dentro al torso fino a bloccarsi contro l’imbottitura sulla schiena.
Se ci aggiungi il cavallo in carica per dare più velocità, magari passano pure imbottitura e cotta sulla schiena, con la punta della lancia da tiro (sempre immaginata aguzza, da sfondamento e lancio tipo freccia bodkin) che sporge tra da dietro. O si ferma prima nel tentativo di spezzare la scapola dopo aver sfondato i polmoni.
Se metti dei bestioni, vengono risultati da bestioni… tipo Zodd, che con la forza che ha in grado di fargli usare a pari velocità uno spadone grosso il doppio di quello che un altro energumeno userebbe, invece di 200 J circa è più giusto orientarsi sui 400.
Non passerà le corazze da 2 mm nemmeno se sono in acciaio di bassa qualità, ma se prende una cotta di maglia ci saranno anelli spezzati che saltano via e imbottitura segata, spezzando via tutte le costole e affondando di qualche cm anche nelle carne, tra le costole fratturate.
La cotta di maglia non è a prova di Zodd. Nemmeno un po’.
Zodd lo conosco appena, ma credo proprio di aver capito. Bene, allora il mio Tempestiano (così ho chiamato i miei simil-vichinghi) farà strage di Cavalieri! Evvai! :D
Grazie Duca, di cuore!
Rimedia subito!
Corri da Zwei a leggere i due capitoli di Zodd…
http://zweilawyer.com/2010/07/08/zodd-e-qui/
… e poi lavati gli occhi con la candeggina: come detto anche da Zwei, in questo stato pre-revisione il voto massimo è quello che darebbe a un romanzo di Licia Troisi. ^_^””
Ahahah! Senz’altro duca! Grazie ancora :D
Premetto che Zodd spakka, yo. C’è da fare un bel lavoro sopra, ma già così apprezzerai.
Quanto alla questione dei bestioni che lanciano dei pila o similaria, direi che è fattibile. Delle salve ben scaglionate potrebbero sfoltire una carica di cavalleria o romperne la formazione, ma i bestioni dovrebbero subito mettersi spalla a spalla e fronteggiare la cavalleria rimanente con un muro di scudi (e le lance puntate verso l’esterno). L’istinto di conservazione dei cavalli li ha sempre portati ad evitare il suicidio contro delle punte di acciaio acuminate.
La questione più spinosa riguarda l’armamento dei bestioni, che sembra variare dall’ascia danese (ascia a due mani), alla spada a due mani (se parliamo di zweihander, quindi di 160-180cm ca, potevano essere utilizzate anche come armi in asta) alla combo lancia (spada)-scudo. Immaginare che un esercito fantasy abbia elaborato delle strategie adatte a sfruttare tutti i pregi di un simile schieramento (e a limitarne i difetti) non è una follia, ma devi essere bravo a capire come si sarebbero schierati effettivamente davanti a una carica di cavalleria.
Zwi, mi conosci già, sono Giacomo (qui mi sono chiamato chris in onore di un mio personaggio). Come vedi raccolgo informazioni sia qui che da te :D
I miei bestioni, così come i cavalieri (non c’è propriamente un buono o un cattivo nella storia, dipende dai punti di vista, perciò amo anche i miei simil-crociati), non hanno mai visto una spada come quella di Zodd. Il massimo è più una spada a una mano e mezza, lunga fra il metro e dieci e il metro e venticinque (sperando di non aver detto misure stupide), ma la portano tutti i crociati.
Ho voluto infatti mantenere la lunghezza massima di un metro per i miei vichinghi, in onore ad un poema nordico (o un testo in prosa, non ricordo adesso) a riguardo del coraggio di un guerriero: Non aver timore del nemico, e mai la tua spada sarà troppo corta!
Addirittura diceva, appunto, che una buona lama non era mai più lunga di un metro. E difatti così ho voluto fare.
La sfida sarà tentare di capire come si sarebbero comportati dei vichinghi nel tentativo di assaltare allo scopo di conquistare e non principalmente di razziare. è vero, in passato vi sono state mire espansionistiche, ma di solito si limitavano ai raid ben conosciuti.
Devo pensare bene a come avrebbero reagito di fronte alla cavalleria pesante. Poi ci sono elementi fantasy che aumentano la difficoltà (o la facilitano a seconda dei casi), su cui però non voglio parlare troppo (sono alquanto geloso sulle mie idee e il pensiero che qualcuno legga su internet e me le rubi è tremendo. ho già detto troppo con vichinghi e cavalieri!).
Comunque ho letto Zodd, c’è in effetti qualcosa da mettere a posto, qualche frase che non mostra abbastanza bene le scene (a volte non riuscivo a seguire l’azione), ma è innegabile: Zodd Spacca! :D
Altro che elfetti con archi lunghi!
Ciao Duca per caso hai qualche dato sulla penetrazione dell’arco composito (modello turco o mongolo)? in pratica mi basterebbe solo sapere se poteva penetrare una maglia di ferro. Grazie in anticipo.
Risposto via mail.
Salve Duca,
dopo aver “assimilato” l’enorme massa di informazioni presenti negli articoli e essendomi produrato buona parte della bibliografia citata (Williams in primis), avrei una domanda storica che mi è venuta leggendo gli Studi sulla Battaglia di Ardant du Picq. Essendo interessanto alla battaglia di Renty (di cui trovo pochissimo in giro), du Picq efferma:
“Una cavalleria corazzata è richiesta chiaramente per motivi morali. Si noti questo per quanto riguarda l’influenza dei cavalieri corazzati sul morale. Alla battaglia di Renty, nel 1554, Tavannes, un maresciallo, aveva con sè la sua compagnia corazzata in acciaio. Era la prima volta che tale armatura era vista. Sostenuto da alcune centinaia di fuggitivi che si erano radunati, si gettò alla testa della sua compagnia, su una colonna di duemila cavalieri tedeschi (che dovrebbero essere stati reiters) che avevano appena gattato sia la fanteria che la cavalleria in disordine. Scelse così bene il tempo che spezzò e respinse questi duemila tedeschi, che caddera all’indietro e disfecero i 1200 cavalieri leggeri che li sostenevano. Ne seguì una fuga generale e la battaglia fu vinta.”
Ora l’affermazione sul tipo della corazza dei gendarmi francesi è senz’altro fuorviante e, per così come è scritta, piuttosto insensata se confrontata con l’evoluzione della corazza di piastre. Probabilmente du Picq usa come fonte le memorie di Tavannes scritte dal figlio, di cui ho copia e su cui penso di aver individuato un simile passo (se il mio arrugginito francese non si sbaglia). La domanda comunque è questa: cosa c’era di speciale (presubilmente) nelle corazze dei gendarmi di Tavannes a Renty, da conferir loro, per lo meno sul loro morale, una certezza di maggior efficacia contro le armi da fuoco?
Non ne ho idea.
Se c’è qualcosa di vero nella vicenda in sé e se il risultato del successo non è dipeso solo dalla sorpresa dell’attacco su una colonna nemica convinta ormai di aver vinto, e scioccata quindi dalla risposta improvvisa da parte di cavalieri appena apparsi…
…forse avevano armature stroardinarie in termini di spessore, ovvero completamente a prova di archibugio?
Nel 1554 non erano ancora comuni come lo sarebbero diventate nella prima metà del ‘600. Dalla tabella di Williams gli spessori delle corazze sono concentrati ancora nella fascia 2-3 mm, con un picco massimo verso 5 mm.
Forse avevano armature con corazza da 5 mm e bracciali e gambali da 3-4 mm, fornendo così un’ottima protezione e la completa invulnerabilità a lame e pistole anche a bruciapelo ovunque (mentre i reiter tedeschi magari avevano armature meno coprenti e meno spesse e i cavalleggeri solo la corazza pettorale e l’elmetto?).
Il discorso sul morale in una carica, leggendo le considerazioni su Renty in Roots of Strategy, sembrano legate alla maggiore robustezza dell’armatura complessiva dei nuovi corazzieri… e quindi la prima apparizione di un nuovo tipo di cavalleria pesante moderna, (quasi) a prova di arma da fuoco, in un mondo in cui picchieri e archibugeri stavano già riducendo molto il ruolo della cavalleria a compiti diversi dalla carica da sfondamento.
Un nuovo tipo di armatura mai vista nel senso di mai vista come “spessore e diffusione” a livello di una intera unità combattente invulnerabile specializzata, secondo me. Il corazziere pesante che sostituisce il vecchio cavaliere e la nuova diffusione dei cavalleggeri e dragoni. Poi non so…
Preso da Google Books:


Ammettendo che il reseconto di Tavannes, poi ripreso da du Picq, sia vero (però non vi è neppure ragione perchè questo detaglio sia totalmente inventato) non sembra che vi sia stata una larga diffussione di una nuova e più spessa corazza negli anni successivi. Ad esempio, dalla testimonianza di La Noue e altri sulle Guerre di Religione sembra che le pistole fossero temuti e mortali negli scontri di cavallaria (che quindi non disponeva ancora di una corazza “alla corazziere”), anche perchè dopo lo scontro iniziale, era assai facile prendersi una palla in una zone meno difesa, tipo la schiena. Magari la compagnia di ordinanza di Tavannes era semplicemente tutta equipaggiata con armature recenti di ottima qualità o spessore importate dalla Germania, mentre in altre compagnie l’equipaggiamento del gendarme era più raffazzonato e quindi non complessivamente altrattanto efficace. Vedro di riprendere il testo di originale di Tavannes.
E’ probabile. Sì, mi sembra più sensato.
buongiorno,duca. vorrei sapere quant’è lo spessore di una armatura di ferro se deve resistere a : un colpo di moschetto del 1600 circa una freccia una spadata di taglio un affondo con la spada un dardo di balestra e un colpo di un mitra moderno. se lei , duca sà rispondermi mi leverebbe tanti dubbi . grazie duca. davide b.
Per ferro puro senza scorie a indebolirlo, usa un W di 0,8-0,9 circa facendo i calcoli con le formule fornite e i commenti già presenti.
Più scorie ci metti e più fa schifo, fino a un W di 0,5 per un ferraccio da munizione impestato e fragile.
Il mitra non era contemplato nei calcoli, ma si può ricavare usando la formula di Krupp. Prendiamo un MP5 da A2 a A5, con 400 m/s alla volata per proiettili da 124 grani 9×19.
Per fermarlo del tutto a bruciapelo servono 2,86 mm di acciaio dolce (AISI 1015-1020, W pari a 1, fracture toughness di 235 KJ/m^2) e quindi 3,3 mm con del ferro del tutto privo di carbonio ma anche di scorie (W a 0,8, 195 KJ/m^2 per il ferro ARMCO).
L’armatura in acciaio dolce sovietica (W 1) per i genieri da combattimento era spessa 2 mm e fermava al 100% il 9×19 degli MP40 a 100 metri. Se ipotizziamo una decelerazione, credibile, nei primi 100 metri di circa 100 m/s, allora bastano effettivamente 1,8 mm (quindi lo blocca senza nemmeno deformarsi in modo troppo lesivo per il geniere).
grazie duca , ma un tronco d’albero invece resiste a un ak47 a una distanza di 100 metri? d.b.
singior duca mi e venuta in mente un altra domanda ,alla quale non trovo risposta.e vista la sua disponibilita gliela faccio a lei :leggendo sopra vedo che e difficilissimo ammazare un cavaliere medievale . e per quanto ne so io per ferire un cavaliere bisognava soltanto prenderlo”a mazzate” con una mazza di ferro(ovviamente intendo un cavaliere ben corazzato e con acciaio di qualita ), ci sono per caso altri modi per ferire o uccidere un cavaliere? d.b.
questo è interessante
http://kenshi247.net/blog/2011/01/28/thoughts-on-tameshigiri-from-famous-swordsmen/
raccoglie due testimonianze sul tameshigiri, la pratica nipponica di esercitare l’arte della spada tagliando diverse cose, matasse di paglia, bamboo, cadaveri, contadini di passaggio e elmetti
si elmetti in particolare nell’ articolo viene riportato lo scritto di Sasaburo Takano uno dei più importanti spadaccini di fine 800, in cui riporta testimonianza di dimostrazioni di taglio su elmetti. Chicca, riferisce che per rendere possibile il taglio gli elmetti venivano riempiti con riso bollito
non è riferito se poi chi tagliava l’elmetto dovesse poi mangiare il riso
Complimenti vivissimi per il sito, questo articolo in special modo l’ho trovato eccezionale, volevo chiederti, dato che con un arma come una grossa ascia o un’alabarda non è possibile tagliare un’armatura a piastre è possibile avere un’idea dell’effetto che il colpo avrebbe sul cavaliere all’interno? in caso di un colpo molto forte è possibile che questo rompa le ossa o è necessario usare un mazza?
Sì, è possibile.
Soprattutto nel caso delle alabarde, dove spesso la lama è piuttosto piccola o sagomata per impattare su una superficie ridotta (forme a mezzaluna o simili), in modo non troppo dissimile dalle flange di una mazza che premono su una ridotta area.
Valutare la capacità di ledere non è facile. Considera che 25 mm di “bozzo” sulla plastilina sottostante sono (o erano anni fa) il massimo tollerato per un giubbotto antiproiettile di classe da IIA a IIIA. Il che significa che nel bloccare i proiettili elencati dalle specifiche NIJ dovevano anche NON deformare in modo eccessivo il supporto. E 25 mm sono una bella botta: se fossero sul cranio, sarebbe una frattura molto pericolosa, e sul torso può essere la rottura o incrinamento di una costola.
Molti giubbotti di alta qualità vantano prestazioni ben al di sotto di quel limite massimo, apposta per garantire che l’impatto risulterà ben distribuito e quindi molto meno doloroso/pericoloso.
Con un’armatura puoi stimare le cose a occhio così (ti faccio un riassunto con quello che ricordo): considera i due valori dell’acciaio, la ultimate tensile strenght e la yield tensile strenght. Il primo indica il valore massimo prima della rottura, il secondo indica il valore massimo prima che inizi a piegarsi in modo grave (nel caso dell’acciaio: una deformazione permanente).
Finché sei sotto il valore yield, la botta sull’armatura non causa un suo piegamento significativo. Magari si flette leggermente, se è il caso, ma torna subito al suo posto. Sopra il valore di yield si piega, ma non si spezza ancora. Prendiamo, non so, un acciaio tipo il C40/AISI 1040 che richiede 500 MPa per la frattura e 350 MPa per piegarsi.
Abbiamo visto che possiamo usare questi valori per stimare la robustezza secondo i testi di Alan Williams, quindi immaginiamo che un certo attrezzo richieda 200 J per penetrare l’armatura… dopo 160 J probabilmente ha già cominciato a piegarla. I restanti 40 J vanno spesi nel piegare l’armatura prima di romperla e in parte finiscono sul corpo di chi è sotto quando l’armatura piegandosi lo “spinge” incrinando ossa e/o mordendo il muscolo.
La questione è quanto un materiale si allunga prima do rompersi e trattandosi di tante leghe diverse non è facile, Secondo eFunda il 1040 ha una elongation del 30,2% che dovrebbe significare (ma non studio queste cose da troppo tempo, per cui se hai un amico che ha fatto di recente Materiali Metallici o corsi simili chiedi conferma) che in un test di frattura allunga fino al 30,2% della sua lunghezza (segnata tra due punti marchiati prima della prova).
http://www.engineersedge.com/material_science/ductility.htm
Però non saprei come farei conti per determinare di quanti cm la piegherà, visto che non sta tirando ma sta spingendo e così ribalta il triangolo ideale su cui andrei a farei conti (la linea colpita viene spinta e diventa l’altezza di un figura la cui sezione verticale è un triangolo isoscele creato dalla spinta) se fosse, non so, una punta di freccia. Boh!
So solo che ci sono acciai, come certi al cromo, con magari 1400 MPa di Yield e 1700 MPa di ultimate con solo 9% elongation e acciaioal manganese da 430-800 con 25% di elongation… e che all’epoca in cui studiarono i primi elemetti si fecero apposta abbondanti spazi di calotta negli elmetti inglesi e americani, di acciaio al manganese piegato a freddo, perché anche se era un acciaio così robusto da resistere con 0,9-1 mm alle stesse botte che venivano fermare da un 1,25 mm crucco al carbonio lavorato con apposite macchine elettriche di piegatura a caldo, allo stesso tempo si piegava di più mentre fermava il colpo, risultando quindi molto pericoloso per il cranio se non dotato in un ampio gioco tra l’imbottitura per calzarlo e la calotta.
Grazie per la risposta, ho ancora un dubbio, i martelli d’arme ad una mano con becco di corvo che si vedono in certi quadri avevano qualche possibilità di perforare un’armatura a piastre o venivano usati solo contro armature “inferiori”?
Sì, è l’arma ideale se non si considerano balestre molto pesanti, archi lunghi per energumeni o armi da fuoco.
Considera che il becco lo puoi considerare per quella che è la sua forma, ovvero assimilabile a una bodkin di calibro più o meno grande.
Calcola l’energia necessaria a forare l’armatura di spessore X e qualità Y con le regole viste prima per le punte bodkin, visto che l’eccellente acciaio del becco si può assimilare alla punta indeformabile usata nei test.
In particolare ti ricordo il paragrafo in cui stimo la possibile energia necessaria per una freccia che abbia il calibro massimo inferiore ai 20 mm (ovvero non superpesante), da cui cito la conclusione per una punta da 18 gradi (13-14 mm ci calibro):
Un buon 140 J sono possibili per un uomo forte, considerando che si stimavano 60-130 J tipici per un uomo “normale”. Un uomo di forza minore è meglio che si concentri magari su le protezioni di braccia e gambe, molto più sottili rispetto a cranio e torso… o colpisca corazze da 2 mm di qualità minore (W 0,75 magari).
L’energumeno che spara bordate sopra i 140 J può fare anche di meglio. Se l’acciaio è davvero pessimo, un ferraccio inguardabile che sta in piedi per miracolo (W 0,5) e la punta molto aguzza e di sezione triangolare o simili (anche solo 8-9 mm di calibro, stile punta di stocco), con un colpo particolarmente forte e perpendicolare alla superficie dell’armatura perfino un elmo da 3 mm potrebbe venire perforato a sufficienza da fratturare il cranio (o potrebbe perforare anche una corazzaccia a prova di pistola poco pesante, sempre da 3 mm in ferraccio). Ma posso solo ipotizzarlo.
Ulteriore vantaggio del becco è l’angolo a 90 gradi rispetto al manico, che riduce un po’ l’enorme difficoltà di infilare un colpo nei varchi ascellari quando il nemico alza le braccia per colpire (in pratica inserendosi nel tempo avversario, o quasi, mentre attacca). Lì essendoci solo le pezze di cotta di maglia, o anche solo l’imbottitura o i vestiti nel ‘500-‘600, il becco entra che un piacere per fare un saluto ai polmoni.
Spero di essere stato utile.
Ciao!
Ovviamente sono solo stime. E magari anche sbagliate. Per un lavoro più serio servirebbe il macchinario e l’utilizzo di punte di calibro diverso contro uno stesso tipo di foglio di acciaio, per stimare l’influenza del solo calibro sull’energia richiesta dalla penetrazione (ci sono paper in vendita nei siti di ricerca sui test con punte “di freccia” contro certi alluminii o acciai, ma costano un sacco di soldi per poche pagine).
Grazie, mi sei stato utilissimo.
Egregio Duca ho letto con molta attenzione gli articoli sulla resistenza delle armature antiche e devo dire che li ho trovati davvero interessanti, fanno giustizia di tante vaccate che sentivo da molti appassionati di rievocazione storica del tipo dardi di balestra che trapassano persone in usbergo di maglia, sella e feriscono anche il cavallo (sic).
Ciao e buone conigliate
Mi sono imbattuta in questo sito per caso e devo proprio dirtelo: lo adoro!
Ci sono un sacco di informazioni utilissime, altro che quello schifo di wikipedia, e mi trovo molto bene ad utilizzarle per le storie che sto scrivendo.
Mi sto approcciando solo ultimamente allo Steampunk e non so molto, anche se è uno stile che mi ha sempre incuriosito. Gli articoli sono interessantissimi e, ancora, davvero utili.
Grazie :D
Felice di esserle stato utile, signorina June95. ^_^
Come ogni signorina per bene dovrebbe fare, ha già letto la mia guida su come si mangia una banana con decoro e dignità?
https://www.steamfantasy.it/blog/2012/10/31/guide-per-signorine-come-si-mangia-una-banana/
Sì, l’avevo già letta in precedenza e adesso non riuscirò più a mangiare una banana senza ridere xD
Ma riderai sommessamente, coprendo la bocca con la delicata manina, come una signorina per bene? ^_^
Mi impegnerò a farlo :D
Spettabilissimo Duca, ho un’altra domanda, mi sapete dire qual’è l’energia ottenibile con una balestra manesca con arco in legno? in rete ho trovato solo informazione molto frammentarie.
Procurati i dati esatti dell’esatta balestra e vedi se riesci a usare questo per ricavare energia fornita, dissipata e ceduta:
https://www.steamfantasy.it/blog/manuali/LONGBOW_E_FISICA_ELEMENTARE.pdf
Se invece intendi l’energia della freccia “alla volata” puoi applicare le informazioni qui sulle equivalenze tra archi e balestre:
https://www.steamfantasy.it/blog/2008/10/20/performance-arco-da-guerra-inglese/
Egregio Dvca, avrei una domanda per quanto riguarda le corazze lamellari utilizzate da Bizantini e Sasanidi. Escludendo l’eventuale strato in cuoio nel quale poggiano le parti metalliche dell’armatura, a parità di qualità dell’acciaio, un’armatura lamellare/a scaglie spessa 1,5 mm ha una resistenza paragonabile ad un’armatura a piastre dello stesso spessore? E se no, guarantisce almeno una maggiore mobilità rispetto alla struttura rigida di un pettorale di piastre oppure è inferiore sotto tutti i punti di vista?
Me lo ero chiesto dopo aver letto che armature di questo tipo vennero utilizzate in Medio Oriente fino al XVII secolo.
Ho cercato sul Web eventuali test condotti su corazze di questo tipo, ma non ne ho trovato traccia.
Saluti dalla Rumelia settentrionale.
Sì. Anzi, operando su piccole lamelle il lavoro è molto più lungo, ma la qualità dell’acciaio può essere garantita meglio anche senza disporre di altiforni (per il discorso sulla difficoltà che cresce al crescere del blumo trattato).
Si perde però il vantaggio del fattore forma perché essendo lamelle unite tra loro con lacci e parziali sovrapposizioni, tenderanno prima a “piegarsi” per la spinta, modificando l’angolo di impatto in uno meno sfavorevole, e solo dopo offriranno autentica resistenza fino a rompersi.
Salve. Girovagavo per il web alla ricerca di siti che si occupano di questioni militari a 360°, e casualmente devo dire mi sono imbattuto in questo sito. Senza essere adulatorio devo dire che mi ha colpito subito. Andando poi a leggere certi articoli specifici di mio interesse, sono rimasto ulteriormente colpito dalla ricchezza di informazioni e riferimenti. La definirei una stesura del sito molto professionale, e anche, difficilmente riscontrabile in molti altri siti, che magari trattano anche o solo di tematiche analoghe. Complimenti.Trovo molto simpatica l’immagine del coniglietto con elmetto tedesco. Sarebbe ancora più divertente un’inquadratura a mezzo busto, con annessa la corazza e lo stemma imperiale germanico. Si creerebbe uno strano paradosso visivo tra l’animo pacifico del coniglietto, e quello, assai più aggressivo e marziale degli uomini che indossavano tale divisa. Una sorta di immagine alla Mrs Bean, in cui non è ben chiaro dove incomincia una cosa, e ne finisce un altra.
Piano piano andrò a girarmi tutto il sito. Saluti. Alex
Egregio Dvca, avrei un altro quesito da porre riguardo le
stramaledettecorazze lamellari (lo ammetto, ho una fissa per l’Impero Ottomano e la Persia dei secoli XV°, XVI°, XVII° nonché XVIII°)Il quesito, per come l’ho formulato, potrebbe contenere un numero discreto di castronerie, ma purtroppo, per quanto mi appassioni l’argomento e per quanto abbia cercato di documentarmi in proposito, il mio livello di ignoranza rimane comunque abbastanza alto. Perdipiù mi rendo conto di scrivere da cani, quindi posso immaginare il perché una domanda attinente sì alla discussione ma solo marginalmente, e scritta pure in malo modo, possa non meritare risposta.
Ordunque:
Ammettiamo che un popolo immaginario -di isolazionisti convinti- abiti una terra immaginaria molto ricca di giacimenti ferrosi, ma non disponga delle risorse o delle competenze tecniche per costruire altiforni. Si trovano a dover fronteggiare invasori tecnologicamente più avanzati, la cui cavalleria ha in dotazione solide corazze di piastre arrotondate invece che le corazze lamellari che usano loro.
In tutta risposta, provano a modificare le loro corazze lamellari per renderle resistenti come le corazze a piastre degli invasori, cercando una soluzione che non comporti un aumento dello spessore dell’armatura.
Potrebbe essere fattibile che arrivino a creare un’armatura lamellare formata da lamelle rivettate e incastrate tra loro in modo rigido come un puzzle (in modo da compensare il più possibile il “fattore forma” avvicinandosi a quello delle corazze a piastre) poggianti su un corpetto di cuoio rinforzato e irrigidito in modo da assumere la stessa curvatura di un’armatura di piastre arrotondata?
E un’armatura del genere raggiungerebbe lo scopo per cui è stata creata o resterebbe comunque inferiore alle sue compari a piastre rigide?
(riguardo la superficie e la disposizione delle lamelle, ma non la curvatura dell’armatura, una cosa del genere: http://www.wojmir9.webd.pl/lamellarsteel01.jpg )
oppure una cosa tipo le Karacena polacche tardo-seicentesche e settecentesche [c’avevano la fissa pure loro ma almeno avevano la scusa del sarmatismo])
Articolo molto bello mi permetto di dissentire solo sulla potenza degli archi moderni. Ovviamente lasciando fuori gli archi olimpici che normalmente sviluppano meno di 60J molti archi compound anche senza libbraggi enormi sono in grado di lanciare le frecce a velocità molto elevate superando con tranquillità i 100J di energia fornita al proietto . Certo essendo le frecce leggere sulla lunga distanza forse conservano meno energia cinetica di un long Bow però a distanze brevi (sino a 90-100 metri) credo possano fornire prestazioni di penetrazione equivalenti… Ovviamente è solo un dettaglio che poco ha a che vedere con la realtà storica che hai descritto così bene. Comunque se ad un certo punto trovo sul campo di tiro uno che mi carica con una cotta di maglia normanna addosso ti dico come è andata a finire.
Matteo
C’è da migliorare la sicurezza del campo se capitano buchi spazio-temporali da cui fuoriescono cavalieri del XII secolo incazzati.
Come quando io, anni fa, ero in fissa che bisognasse montare la baionetta sugli eReader perché se mentre leggi sbuca fuori un soldato francese col cappotto blu che ti vuole baionettare come si fa? Eh!
La sicurezza prima di tutto!
Beh per adesso il reticolo spazio tempo sembra tenere… certo il desiderio di infrangere la barriera spazio temporale e portare una compagnia di arceri armati di modernissimi compound ad affrontare dei fucilieri inglesi dell’epoca della guerra d’indipendenza americana per distruggerli per cadenza di tiro e precisione è una tara di cui è difficile liberarsi…
signor duca buongiorno , le volevo rivolgere una semplice ( e forse banale ) domanda : lei sa più o meno di che materiale erano fatte le uniformi inglesi del 1700-1800 ? in somma le famose giubbe rosse di che erano fatte ?
grazie mille in anticipo !
D.B.
Lana. Usa Wikipedia:
http://en.wikipedia.org/wiki/Red_coat_%28British_army%29#Material_used
signor duca grazie mille della risposta , comunque la informo che io avevo utilizzato wikipedia ma GIURO non avevo trovato niente , grazie mille ancore e buona serata !
D.B.
Signor Duca, complimenti per l’accuratezza e la serietà tecnica dell’articolo.
Riguardo ai test sulle spade, in effetti non era possibile danneggiare con un fendente un’armatura;
Infatti molte delle spade medioevali non erano neanche affiliate, o lo erano solo in alcuni punti.
Ho avuto modo di praticare, dopo molti anni di Kung Fu, un’anno di Kali, arte marziale filippina ma che deve molto del suo bagaglio tecnico alla scherma Medioevale; i Filippini hanno copiato molte delle tecniche dai colonizzatori Portoghesi.
Gli attacchi con la spada venivano praticati di punta, punta disegnata per lo sfondamento, spesso afferrando con la mano il primo terzo della lama, detto ricasso, non affilato, per rinforzare ulteriormente il colpo.
Quindi bisognerebbe capire se la punta di una spada può forare una corazza, o gli affondi erano portati con precisione solo ai punti deboli dell’armatura, cosa comunque non possibile con un fendente.
Va anche detto che, essendo spesso non affiliate neanche sulla punta, ma solo nella parte mediana, le spade potevano essere afferrate al contrario per colpire a mo’ di martello da guerra, con I bracci dell’elsa, spesso appuntiti.
Un esauriente manuale dell’epoca è il “flos duellatorum” di fiore dei liberi (attorno al 1350).
Ciao, ho trovato interessante soprattutto (ma non solo, ovviamente) questo tratto dell’articolo:
Mi chiedevo però, se con colpi d’armi bianche, più che altro le mazze, si potessero spezzare le ossa dell'”indossatore”.
Me lo chiedevo perchè io faccio il fabbro e sebbene lavori il ferro e non l’acciaio, per quanto resistente possa essere le struttura in ferro che colpisco col mio martello, la superficie su cui poggia spesso e volentieri subisce danni…
Ciao.
Se il metallo non si piega, l’effetto non è rilevante. Devi considerare la differenza tra un corpo libero e uno vincolato: l’umano è libero, se lo colpisci fornisci una botta a cui, se l’arma non lo attraversa tramutando la spinta in tagli o perforazione, corrisponde solo del calore per attrito e una spinta (un nuovo sistema in cui la quantità di moto disponibile è la stessa, ma invece di esserci solo l’arma a muoversi c’è anche l’ostacolo da spingere).
Se l’oggetto è vincolato a terra e lo colpisci, il vincolo reagisce con effetto uguale e contrario al movimento che nega (il corpo quindi non sfugge, spinto dal colpo, ma lo incassa tutto). La differenza tra, per dire, dare un pugno nello stomaco a un tizio in piedi o darglielo mentre è sdraiato su un pavimento di marmo.
Nel caso dei metalli hai due valori di Tensile Strength da tenere in conto, principali: lo Yield indica dopo quanto inizia a piegarsi, la Massima indica dopo quanto si spezza. Un acciaio con 500 Mpa di massima può avere 400 Mpa di Yield, per esempio. Gli acciai al manganese hanno divari ancora più alti (1200 a 400, tipo), per questo gli elmetti M1 americani avevano bisogno di uno spazio d’aria ancora maggiore tra calotta e cranio, se no l’elmetto si piegava, senza rompersi, ma il cranio si spezzava!
Va poi aggiunto il valore con cui si piegano, ovvero quei MPa tra i due valori a quanto allungamento portano… può essere tanto (acciai al manganese) o poco (acciai inossidabili, più proni al rompersi che al piegarsi) ed è un fattore in più rispetto agli MPa: se tra quel 400 e il 500 ci sono, non so, mezzo cm di bozzo è una cosa… se sono 2 cm è un’altra.
La stessa regola si applica sui giubbotti antiproiettile, per valutare se difendono chi lo indossa o se pur non venendo perforati dal proiettile ammazzano chi è dentro: se l’effetto sulla plastilina che indossa il giubbotto è inferiore a 2,5 cm, la protezione è corretta e i danni minimi (una costola incrinata, un ematoma). Immagina come sarebbe inutile come armatura, se esistesse, un velo impenetrabile a qualsiasi colpo, ma che si piega e si dilata come un chewing gum: il proiettile viene avvolto dal velo e prosegue indisturbato, perforando il tizio. ^_^
La gran parte dei giubbotti di qualità in classe IIIA ha deformazioni inferiori, meno della metà (spesso 1 cm o poco più): un pugno, in pratica, e un piccolo livido.
signor duca buona sera , le volevo rivolgere solo una domanda : ma più o meno quanto tempo ci voleva nel XV secolo per fabbricare un armatura completa ? la mia è solo una curiosità perché io ho sentito anche che alcune armature venivano fabbricate anche in 3-4 mesi ! e la cosa mi sembra strana .
grazie mille in anticipo
D.B.
innanzitutto complimenti per l’articolo molto interessante ed esauriente
Mi è sorto un dubbio però sulla prova di penetrazione effettuata con il Rosand IFW5 riguardo i proiettili. durante la prova è stato utilizzato un finto proiettile in acciaio al posto del piombo, si è tenuto conto della differenza di peso specifico tra i due materiali?
Perchè, per il poco che conosco di balistica, un proiettile di pari dimensione ma con un peso specifico maggiore crea un danno maggiore (un esempio sono i proiettili all’uranio impoverito usati nelle armi controcarro ) o sbaglio?
La densità sezionale è irrilevante al fine della valutazione, non influenza le formule di penetrazione delle armature (es: formula di Krupp) in cui conta solo l’energia cinetica. La densità sezionale influenza le formule di attraversamento di mezzi molto più teneri, praticamente fluidi (aria, acqua, carne), in modo quasi algebrico se ricordo giusto (perlomeno in aria e acqua sì) e in cui conta più la quantità di moto che l’energia cinetica.
Di cosa sia fatta una sfera di 20 mm, purché non sia troppo più molle di ciò che colpisce, non influenza le formule. Se molto molle, come il piombo non incamiciato rispetto a una lastra di acciaio AISI 1025, vi sono differenze di penetrazione rispetto a un proiettile indeformabile (molto più duro del mezzo che attraverserà) o che si deforma solo quando la sua energia cinetica residua è inferiore al 10% (normale FMJ).
Sebbene mi sia dura capire quanta forza fisicamente sia necessaria per scoccare una freccia sufficiente a penetrare i famosi 5 mm di buff coat, ti ringrazio molto dell’articolo, accurato, interessante e utilissimo per scrivere con un po’ di cognizione di materia fantastica ;) ce ne vorrebbero tanti, di articoli così!
Grazie!
Per penetrare la buff coat da 5 mm sono indicati circa 30 J. Una cifra molto modesta, considerando che da archi da guerra lunghi da 100-150 libbre ci aspettiamo 90-150 J allo scoccare (in base a peso delle frecce e alla lunghezza di apertura dell’arco, di solito 30-32 pollici in mano a uomini non bassi).
https://www.steamfantasy.it/blog/2008/10/20/performance-arco-da-guerra-inglese/
A pochi metri di distanza, a quanto dicono qui http://ballista.wikia.com/wiki/Personal_torsion_weapons , bastano anche solo un arco da 60 libbre con 28 pollici di apertura (che va benissimo per la caccia). Con frecce da 32,5 grammi ottiene 49,72 m/s e quindi 40 J, sufficienti a bucare il cuoio e iniziare a penetrare il corpo (solo 10 J, non entrerà molto, ma se c’è del veleno e sotto i vestiti non oppongono resistenza può arrivare a contatto).
Meglio archi più forti. Ma già 60 libbre richiedono un fisico in forma e abitudine all’uso per aprirlo bene, anche se siamo molto distanti dai libbraggi di archi da guerra davvero pericolosi (e maneggiati da energumeni specializzati).
Non so se migliora la situazione usando frecce più pesanti, magari 32,5 grammi è troppo poco per esprimere al meglio un arco da 60 libbre?
“Una superficie così piccola e aguzza da sembrare una freccia da sfondamento, come, uh, un Estoc?
In tal caso credo si possa stimare che l’energia necessaria per penetrare di 40 mm sia la stessa che per le frecce da sfondamento: 55 J (40 J per iniziare a penetrare). Va poi considerato se il cosciale è arrotondato o spigolato (o se magari è arrotondato, ma l’impatto arriva a 90 gradi è come se non lo fosse)
Williams per lance, asce, spade ecc… stimava da un uomo normale (non un bestione) energie di 60-130 J. Direi quindi che sembrerebbe fattibile.”
Volevo chiedere, riguardo a questo caso particolare, come è stata stimata la forza in Joule generata da un uomo normale ? perchè i muscoli utilizzati per un affondo sono molto diversi da quelli utilizzati per un fendente (solo braccio contro braccio+spalla+pettorale o dorsale) …a mio avviso ci dovrebbe essere una notevole differenza (anche gli strumenti da lavoro come asce o piccozze sfruttano questa differenza… anche le seghe compiono il lavoro maggiore durante il “ritorno” piuttosto che durante la spinta).
In secondo luogo, credo (parere personalissimo) che se si vuol considerare la capacità di penetrare una corazza bisognerebbe tener anche della velocità con cui arriva il colpo e quindi della sua capacità di scalfire o quantomeno intaccare il metallo della piastra nel primissimo momento dell’ impatto per creare un “avvallamento” che permetta al colpo di scaricare poi tutta la sua forza senza far “strisciare” il punto d’impatto, cosa che avviene con palle, frecce, quadrelli o piccozze… ma suppongo molto meno con armi da punta ma a minore velocità quali lance ed estoc che (a mio avviso) avrebbero avuto una maggior propensione a scivolare su una corazza impattata non perfettamente a 90° .
Un ultima nota… ricordo una trasmissione su History Channel dove un metallurgo spiegava come anche la dimensione della piastra doveva essere presa in considerazione, infatti una freccia che riusciva a perforare una corazza di 30×30 cm rimbalzava bellamente se colpiva una corazza identica (spessore e materiale) ma con una superficie di 4×4 cm (in pratica una “scaglia”) …lì spiegavano che era un effetto dovuto alla distribuzione dell’onda d’urto… ma poi… non saprei.
Scrivi ad Alan Williams, l’autore del libro.
L’energia è data dal quadrato della velocità per la massa. Se usi l’energia, stai considerando in modo enorme l’importanza della velocità all’impatto prima che la resistenza dell’armatura “freni” il colpo. In casi diversi, con tessuti soffici (balistica terminale), si tende invece a usare maggiormente la quantità di moto o comunque a non dare alla velocità un’importanza superiore rispetto alla massa.
Come già visto nell’articolo.
Tutto già dettagliatamente spiegato nell’articolo, che parla di colpi perpendicolari (caso ideale) e fornisce stime tipiche di angoli di impatto da considerare su armature tondeggianti (milanese) o spigolate (massimiliana), tramite angoli tipici di 30 e 45 gradi per ricalcolare l’energia necessaria alla penetrazione di un colpo “ben piazzato”.